2024年高考数学甲卷-理6(5分)设函数$f(x)=\dfrac{{e}^{x}+2\sin x}{1+{x}^{2}}$,则曲线$y=f(x)$在点$(0,1)$处的切线与坐标轴围成的三角形的面积为( )
A.$\dfrac{1}{6}$ B.$\dfrac{1}{3}$ C.$\dfrac{1}{2}$ D.$\dfrac{2}{3}$【答案详解】 |
2024年高考数学甲卷-理7(5分)函数$f(x)=-x^{2}+(e^{x}-e^{-x})\sin x$ 的区间$[-2.8$,$2.8]$的图像大致为( )
A.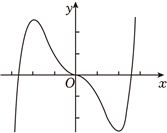
B.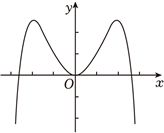
C. 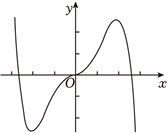
D.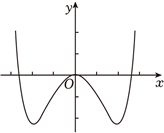 【答案详解】 【答案详解】 |
2024年高考数学甲卷-理8(5分)已知$\dfrac{\cos \alpha }{\cos \alpha -\sin \alpha }=\sqrt{3}$,则$\tan (\alpha +\dfrac{\pi }{4})=$( )
A.$2\sqrt{3}+1$ B.$2\sqrt{3}-1$ C.$\dfrac{\sqrt{3}}{2}$ D.$1-\sqrt{3}$【答案详解】 |
2024年高考数学甲卷-理9(5分)已知向量$\overrightarrow{a}=(x+1,x)$,$\overrightarrow{b}=(x,2)$,则$($ $)$
A.“$\overrightarrow{a}\bot \overrightarrow{b}$”的必要条件是“$x=-3$”
B.“$\overrightarrow{a}//\overrightarrow{b}$”的必要条件是“$x=-3$”
C.“$\overrightarrow{a}\bot \overrightarrow{b}$”的充分条件是“$x=0$”
D.“$\overrightarrow{a}//\overrightarrow{b}$”的充分条件是“$x=-1+\sqrt{3}$”【答案详解】 |
2024年高考数学甲卷-理10(5分)已知$\alpha$、$\beta$是两个平面,$m$、$n$是两条直线,$\alpha \bigcap \beta =m$.下列四个命题:
①若$m//n$,则$n//\alpha$或$n//\beta$
②若$m\bot n$,则$n\bot \alpha$,$n\bot \beta$
③若$n//\alpha$,且$n//\beta$,则$m//n$
④若$n$与$\alpha$和$\beta$所成的角相等,则$m\bot n$
其中,所有真命题的编号是$($ $)$
A.①③ B.②③ C.①②③ D.①③④【答案详解】 |

