2023年高考数学甲卷-理16(5分)在$\Delta ABC$中,$\angle BAC=60^\circ$,$AB=2$,$BC=\sqrt{6}$,$D$为$BC$上一点,$AD$为$\angle BAC$的平分线,则$AD=$____.
【答案详解】 |
2023年高考数学甲卷-理17(12分)已知数列$\{a_{n}\}$中,$a_{2}=1$,设$S_{n}$为$\{a_{n}\}$前$n$项和,$2S_{n}=na_{n}$.
(1)求$\{a_{n}\}$的通项公式;
(2)求数列$\{\dfrac{{a}_{n}+1}{{2}^{n}}\}$的前$n$项和$T_{n}$.【答案详解】 |
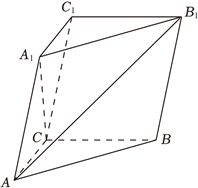
2023年高考数学甲卷-理18(12分)在三棱柱$ABC-A_{1}B_{1}C_{1}$中,$AA_{1}=2$,$A_{1}C\bot$底面$ABC$,$\angle ACB=90^\circ$,$A_{1}$到平面$BCC_{1}B_{1}$的距离为1.
(1)求证:$AC=A_{1}C$;
(2)若直线$AA_{1}$与$BB_{1}$距离为2,求$AB_{1}$与平面$BCC_{1}B_{1}$所成角的正弦值.
【答案详解】 |
2023年高考数学甲卷-理19(12分)一项试验旨在研究臭氧效应,试验方案如下:选40只小白鼠,随机地将其中20只分配到试验组,另外20只分配到对照组,试验组的小白鼠饲养在高浓度臭氧环境,对照组的小白鼠饲养在正常环境,一段时间后统计每只小白鼠体重的增加量(单位:$g)$.
(1)设$X$表示指定的两只小鼠中分配到对照组的只数,求$X$的分布列和数学期望;
(2)试验结果如下:
对照组的小白鼠体重的增加量从小到大排序为
15.2 18.8 20.2 21.3 22.5 23.2 25.8 26.5 27.5 30.1
32.6 34.3 34.8 35.6 35.6 35.8 36.2 37.3 40.5 43.2
试验组的小白鼠体重的增加量从小到大排序为
7.8 9.2 11.4 12.4 13.2 15.5 16.5 18.0 18.8 19.2
19.8 20.2 21.6 22.8 23.6 23.9 25.1 28.2 32.3 36.5
$(i)$求40只小白鼠体重的增加量的中位数$m$,再分别统计两样本中小于$m$与不小于$m$的数据的个数,完成如下列联表:| | $ < m$ | $\geqslant m$ | | 对照组 | | | | 实验组 | | |
$(ii)$根据$(i)$中的列联表,能否有$95%$的把握认为小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量有差异?
附:$K^{2}=\dfrac{n{{(ad-bc)}^2}}{({a+b})({c+d})({a+c})({b+d})}$,| $P(K^{2}\geqslant k)$ | 0.100 | 0.050 | 0.010 | | $k$ | 2.706 | 3.841 | 6.635 |
【答案详解】 |
2023年高考数学甲卷-理20(12分)设抛物线$C:y^{2}=2px(p > 0)$,直线$x-2y+1=0$与$C$交于$A$,$B$两点,且$\vert AB\vert =4\sqrt{15}$.
(1)求$p$的值;
(2)$F$为$y^{2}=2px$的焦点,$M$,$N$为抛物线上的两点,且$\overrightarrow{MF}\cdot \overrightarrow{NF}=0$,求$\Delta MNF$面积的最小值.【答案详解】 |

