2024年高考数学新高考Ⅰ-16(15分)已知$A(0,3)$和$P(3,\dfrac{3}{2})$为椭圆$C:\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1(a > b > 0)$上两点.
(1)求$C$的离心率;
(2)若过$P$的直线$l$交$C$于另一点$B$,且$\Delta ABP$的面积为9,求$l$的方程.
【答案详解】 |
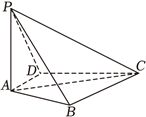
2024年高考数学新高考Ⅰ-17(15分)如图,四棱锥$P-ABCD$中,$PA\bot$底面$ABCD$,$PA=AC=2$,$BC=1$,$AB=\sqrt{3}$.
(1)若$AD\bot PB$,证明:$AD//$平面$PBC$;
(2)若$AD\bot DC$,且二面角$A-CP-D$的正弦值为$\dfrac{\sqrt{42}}{7}$,求$AD$.
【答案详解】 |
2024年高考数学新高考Ⅰ-18(17分)已知函数$f(x)=\ln \dfrac{x}{2-x}+ax+b(x-1)^{3}$.
(1)若$b=0$,且$f\prime (x)\geqslant 0$,求$a$的最小值;
(2)证明:曲线$y=f(x)$是中心对称图形;
(3)若$f(x) > -2$当且仅当$1 < x < 2$,求$b$的取值范围.
【答案详解】 |
2024年高考数学新高考Ⅰ-19(17分)设$m$为正整数,数列$a_{1}$,$a_{2}$,$\ldots$,$a_{4m+2}$是公差不为0的等差数列,若从中删去两项$a_{i}$和$a_{j}(i < j)$后剩余的$4m$项可被平均分为$m$组,且每组的4个数都能构成等差数列,则称数列$a_{1}$,$a_{2}\ldots$,$a_{4m+2}$是$(i,j)$——可分数列.
(1)写出所有的$(i,j)$,$1\leqslant i < j\leqslant 6$,使数列$a_{1}$,$a_{2}$,$\ldots$,$a_{6}$是$(i,j)$——可分数列;
(2)当$m\geqslant 3$时,证明:数列$a_{1}$,$a_{2}$,$\ldots$,$a_{4m+2}$是$(2,13)$——可分数列;
(3)从1,2,$\ldots$,$4m+2$中一次任取两个数$i$和$j(i < j)$,记数列$a_{1}$,$a_{2}$,$\ldots$,$a_{4m+2}$是$(i,j)$——可分数列的概率为$P_{m}$,证明:$P_{m} > \dfrac{1}{8}$.
【答案详解】 |

