|
2024年高考数学新高考Ⅰ-11<-->2024年高考数学新高考Ⅰ-13
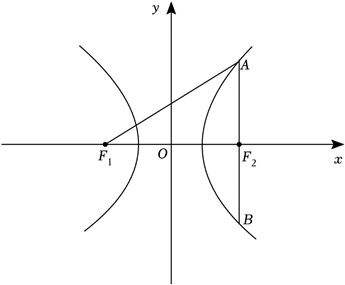
(5分)设双曲线$C:\dfrac{{x}^{2}}{{a}^{2}}-\dfrac{{y}^{2}}{{b}^{2}}=1(a > 0,b > 0)$的左、右焦点分别为$F_{1}$,$F_{2}$,过$F_{2}$作平行于$y$轴的直线交$C$于$A$,$B$两点,若$\vert F_{1}A\vert =13$,$\vert AB\vert =10$,则$C$的离心率为____.
答案:$\dfrac{3}{2}$.
分析:由题意求出$\vert F_{1}A\vert$,$\vert F_{2}A\vert$,利用双曲线的定义求出$a$和$b^{2}$、$c$,即可求出双曲线$C$的离心率.
解:由题意知,$\vert F_{1}A\vert =13$,$\vert F_{2}A\vert =\dfrac{1}{2}\vert AB\vert =5$,
所以$\vert F_{1}A\vert -\vert F_{2}A\vert =2a=8$,解得$a=4$;
又$x=c$时,$y=\dfrac{{b}^{2}}{a}$,即$\vert F_{2}A\vert =\dfrac{{b}^{2}}{a}=5$,
所以$b^{2}=5a=20$,
所以$c^{2}=a^{2}+b^{2}=16+20=36$,所以$c=6$,
所以双曲线$C$的离心率为$e=\dfrac{c}{a}=\dfrac{3}{2}$.
故答案为:$\dfrac{3}{2}$.
点评:本题考查了双曲线的定义与应用问题,也考查了数学运算核心素养,是基础题.
2024年高考数学新高考Ⅰ-11<-->2024年高考数学新高考Ⅰ-13
全网搜索"2024年高考数学新高考Ⅰ-12"相关
|

