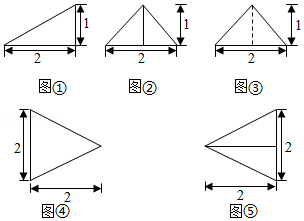
2021年高考数学乙卷-理16(5分)以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为______(写出符合要求的一组答案即可).
 【答案详解】 【答案详解】 |
2021年高考数学乙卷-理17(12分)某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
| 旧设备 | 9.8 | 10.3 | 10.0 | 10.2 | 9.9 | 9.8 | 10.0 | 10.1 | 10.2 | 9.7 | | 新设备 | 10.1 | 10.4 | 10.1 | 10.0 | 10.1 | 10.3 | 10.6 | 10.5 | 10.4 | 10.5 |
旧设备和新设备生产产品的该项指标的样本平均数分别记为$\overline{x}$和$\overline{y}$,样本方差分别记为$s_{1}^{2}$和$s_{2}^{2}$.
(1)求$\overline{x}$,$\overline{y}$,$s_{1}^{2}$,$s_{2}^{2}$;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果$\overline{y}-\overline{x}\geqslant 2\sqrt{\dfrac{{s}_{1}^{2}{+s}_{2}^{2}}{10}}$,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).【答案详解】 |
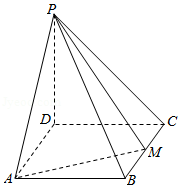
2021年高考数学乙卷-理18(12分)如图,四棱锥$P-ABCD$的底面是矩形,$PD\bot$底面$ABCD$,$PD=DC=1$,$M$为$BC$中点,且$PB\bot AM$.
(1)求$BC$;
(2)求二面角$A-PM-B$的正弦值.
 【答案详解】 【答案详解】 |
2021年高考数学乙卷-理19记$S_{n}$为数列$\{a_{n}\}$的前$n$项和,$b_{n}$为数列$\{S_{n}\}$的前$n$项积,已知$\dfrac{2}{{S}_{n}}+\dfrac{1}{{b}_{n}}=2$.
(1)证明:数列$\{b_{n}\}$是等差数列;
(2)求$\{a_{n}\}$的通项公式.【答案详解】 |
2021年高考数学乙卷-理20已知函数$f(x)=ln(a-x)$,已知$x=0$是函数$y=xf$$(x)$的极值点.
(1)求$a$;
(2)设函数$g(x)=\dfrac{x+f(x)}{xf(x)}$.证明:$g(x)<1$.【答案详解】 |

