|
2021年高考数学乙卷-理4<-->2021年高考数学乙卷-理6
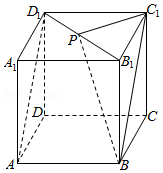
5.(5分)在正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中,$P$为$B_{1}D_{1}$的中点,则直线$PB$与$AD_{1}$所成的角为( )
A.$\dfrac{\pi }{2}$ B.$\dfrac{\pi }{3}$ C.$\dfrac{\pi }{4}$ D.$\dfrac{\pi }{6}$
分析:由$AD_{1}//BC_{1}$,得$\angle PBC_{1}$是直线$PB$与$AD_{1}$所成的角(或所成角的补角),由此利用余弦定理,求出直线$PB$与$AD_{1}$所成的角.
解$\because AD_{1}//BC_{1}$,$\therefore \angle PBC_{1}$是直线$PB$与$AD_{1}$所成的角(或所成角的补角),
设正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$的棱长为2,
则$PB_{1}=PC_{1}=\dfrac{1}{2}\sqrt{{2}^{2}+{2}^{2}}=\sqrt{2}$,$BC_{1}=\sqrt{{2}^{2}+{2}^{2}}=2\sqrt{2}$,$BP=\sqrt{{2}^{2}+(\sqrt{2})^{2}}=\sqrt{6}$,
$\therefore \cos \angle PBC_{1}=\dfrac{P{B}^{2}+B{{C}_{1}}^{2}-P{{C}_{1}}^{2}}{2\times PB\times B{C}_{1}}=\dfrac{6+8-2}{2\times \sqrt{6}\times 2\sqrt{2}}=\dfrac{\sqrt{3}}{2}$,
$\therefore \angle PBC_{1}=\dfrac{\pi }{6}$,
$\therefore$直线$PB$与$AD_{1}$所成的角为$\dfrac{\pi }{6}$.
故选:$D$.
点评:本题考查异面直线所成角和余弦定理,考查运算求解能力,是基础题.
2021年高考数学乙卷-理4<-->2021年高考数学乙卷-理6
全网搜索"2021年高考数学乙卷-理5"相关
|

