|
2021年高考数学乙卷-理17<-->2021年高考数学乙卷-理19
18.(12分)如图,四棱锥$P-ABCD$的底面是矩形,$PD\bot$底面$ABCD$,$PD=DC=1$,$M$为$BC$中点,且$PB\bot AM$.
(1)求$BC$;
(2)求二面角$A-PM-B$的正弦值.
分析:(1)连结$BD$,利用线面垂直的性质定理证明$AM\bot PD$,从而可以证明$AM\bot$平面$PBD$,得到$AM\bot BD$,证明$\rm{Rt}\Delta DAB\backsim \rm{Rt}\Delta ABM$,即可得到$BC$的长度;
(2)建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,然后利用待定系数法求出平面的法向量,由向量的夹角公式以及同角三角函数关系求解即可.
解:(1)
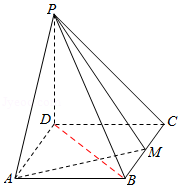
连结$BD$,因为$PD\bot$底面$ABCD$,且$AM\subset$平面$ABCD$,
则$AM\bot PD$,又$AM\bot PB$,$PB\bigcap PD=P$,$PB$,$PD\subset$平面$PBD$,
所以$AM\bot$平面$PBD$,又$BD\subset$平面$PBD$,则$AM\bot BD$,
所以$\angle ABD+\angle ADB=90\circ$,又$\angle ABD+\angle MAB=90\circ$,
则有$\angle ADB=\angle MAB$,所以$\rm{Rt}\Delta DAB\backsim \rm{Rt}\Delta ABM$,
则$\dfrac{AD}{AB}=\dfrac{BA}{BM}$,所以$\dfrac{1}{2}B{C}^{2}=1$,解得$BC=\sqrt{2}$;
(2)因为$DA$,$DC$,$DP$两两垂直,故以点$D$位坐标原点建立空间直角坐标系如图所示,

则$A(\sqrt{2},0,0),B(\sqrt{2},1,0),M(\dfrac{\sqrt{2}}{2},1,0)$,$P(0$,0,$1)$,
所以$\overrightarrow{AP}=(-\sqrt{2},0,1)$,$\overrightarrow{AM}=(-\dfrac{\sqrt{2}}{2},1,0),\overrightarrow{BM}=(-\dfrac{\sqrt{2}}{2},0,0),\overrightarrow{BP}=(-\sqrt{2},-1,1)$,
设平面$AMP$的法向量为$\overrightarrow{n}=(x,y,z)$,
则有$\left\{\begin{array}{l}{\overrightarrow{n}\cdot \overrightarrow{AP}=0}\\ {\overrightarrow{n}\cdot \overrightarrow{AM}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{-\sqrt{2}x+z=0}\\ {-\dfrac{\sqrt{2}}{2}x+y=0}\end{array}\right.$,
令$x=\sqrt{2}$,则$y=1$,$z=2$,故$\overrightarrow{n}=(\sqrt{2},1,2)$,
设平面$BMP$的法向量为$\overrightarrow{m}=(p,q,r)$,
则有$\left\{\begin{array}{l}{\overrightarrow{m}\cdot \overrightarrow{BM}=0}\\ {\overrightarrow{m}\cdot \overrightarrow{BP}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{-\dfrac{\sqrt{2}}{2}p=0}\\ {-\sqrt{2}p-q+r=0}\end{array}\right.$,
令$q=1$,则$r=1$,故$\overrightarrow{m}=(0,1,1)$,
所以$\vert \cos <\overrightarrow{n},\overrightarrow{m}>\vert =\dfrac{\vert \overrightarrow{n}\cdot \overrightarrow{m}\vert }{\vert \overrightarrow{n}\vert \vert \overrightarrow{m}\vert }=\dfrac{3}{\sqrt{7}\times \sqrt{2}}=\dfrac{3\sqrt{14}}{14}$,
设二面角$A-PM-B$的平面角为$\alpha$,
则$\sin \alpha =\sqrt{1-co{s}^{2}\alpha }=\sqrt{1-co{s}^{2}<\overrightarrow{n},\overrightarrow{m}>}=\sqrt{1-(\dfrac{3\sqrt{14}}{14})^{2}}=\dfrac{\sqrt{70}}{14}$,
所以二面角$A-PM-B$的正弦值为$\dfrac{\sqrt{70}}{14}$.
点评:本题考查了空间中线段长度求解以及二面角的求解,在求解有关空间角问题的时候,一般会建立合适的空间直角坐标系,将空间角问题转化为空间向量问题进行研究,属于中档题.
2021年高考数学乙卷-理17<-->2021年高考数学乙卷-理19
全网搜索"2021年高考数学乙卷-理18"相关
|

