2023年高考数学乙卷-文16(5分)已知点$S$,$A$,$B$,$C$均在半径为2的球面上,$\Delta ABC$是边长为3的等边三角形,$SA\bot$平面$ABC$,则$SA=$____.
【答案详解】 |
2023年高考数学乙卷-文17(12分)某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后的橡胶产品的伸缩率,甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为$x_{i}$,$y_{i}(i=1$,2,$\ldots 10)$.试验结果如下:| 试验序号$i$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | 伸缩率$x_{i}$ | 545 | 533 | 551 | 522 | 575 | 544 | 541 | 568 | 596 | 548 | | 伸缩率$y_{i}$ | 536 | 527 | 543 | 530 | 560 | 533 | 522 | 550 | 576 | 536 |
记$z_{i}=x_{i}-y_{i}(i=1$,2,$\dotsb$,$10)$,记$z_{1}$,$z_{2}$,$\dotsb$,$z_{10}$的样本平均数为$\overline{z}$,样本方差为$s^{2}$.
(1)求$\overline{z}$,$s^{2}$;
(2)判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高.(如果$\overline{z}\geqslant 2\sqrt{\dfrac{s^2}{10}}$,则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高,否则不认为有显著提高)【答案详解】 |
2023年高考数学乙卷-文18(12分)记$S_{n}$为等差数列$\{a_{n}\}$的前$n$项和,已知$a_{2}=11$,$S_{10}=40$.
(1)求$\{a_{n}\}$的通项公式;
(2)求数列$\{\vert a_{n}\vert \}$的前$n$项和$T_{n}$.【答案详解】 |
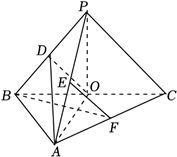
2023年高考数学乙卷-文19(12分)如图,在三棱锥$P-ABC$中,$AB\bot BC$,$AB=2$,$BC=2\sqrt{2}$,$PB=PC=\sqrt{6}$,$BP$,$AP$,$BC$的中点分别为$D$,$E$,$O$,点$F$在$AC$上,$BF\bot AO$.
(1)求证:$EF//$平面$ADO$;
(2)若$\angle POF=120^\circ$,求三棱锥$P-ABC$的体积.
 【答案详解】 【答案详解】 |
2023年高考数学乙卷-文20(12分)已知函数$f(x)=(\dfrac{1}{x}+a)\ln (1+x)$.
(1)当$a=-1$时,求曲线$y=f(x)$在点$(1$,$f(x))$处的切线方程;
(2)若函数$f(x)$在$(0,+\infty )$单调递增,求$a$的取值范围.【答案详解】 |

