|
2023年高考数学乙卷-文15<-->2023年高考数学乙卷-文17
(5分)已知点$S$,$A$,$B$,$C$均在半径为2的球面上,$\Delta ABC$是边长为3的等边三角形,$SA\bot$平面$ABC$,则$SA=$____.
答案:2.
分析:先用正弦定理求底面外接圆半径,再结合直棱柱的外接球及球的性质能求出结果.
解:设$\Delta ABC$的外接圆圆心为$O_{1}$,半径为$r$,
则$2r=\dfrac{AB}{\sin \angle ACB}=\dfrac{3}{\dfrac{\sqrt{3}}{2}}=2\sqrt{3}$,解得$r=\sqrt{3}$,
设三棱锥$S-ABC$的外接球球心为$O$,连接$OA$,$OO_{1}$,
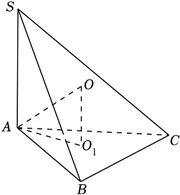
则$OA=2$,$OO_{1}=\dfrac{1}{2}SA$,
$\because$$O{A}^{2}=O{{O}_{1}}^{2}+{O}_{1}{A}^{2}$,$\therefore 4=3+\dfrac{1}{4}S{A}^{2}$,解得$SA=2$.
故答案为:2.
点评:本题考查正弦定理、三角形外接圆半径,直棱柱的外接球及球的性质等基础知识,考查运算求解能力,是中档题.
2023年高考数学乙卷-文15<-->2023年高考数学乙卷-文17
全网搜索"2023年高考数学乙卷-文16"相关
|

