2021年高考数学北京16已知在$\Delta ABC$中,$c=2b\cos B$,$C=\dfrac{2\pi }{3}$.
(1)求$B$的大小;
(2)在三个条件中选择一个作为已知,使$\Delta ABC$存在且唯一确定,并求$BC$边上的中线的长度.
①$c=\sqrt{2}b$;②周长为$4+2\sqrt{3}$;③面积为$S_{\Delta ABC}=\dfrac{3\sqrt{3}}{4}$.【答案详解】 |
2021年高考数学北京17已知正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$,点$E$为$A_{1}D_{1}$中点,直线$B_{1}C_{1}$交平面$CDE$于点$F$.
(1)求证:点$F$为$B_{1}C_{1}$中点;
(2)若点$M$为棱$A_{1}B_{1}$上一点,且二面角$M-CF-E$的余弦值为$\dfrac{\sqrt{5}}{3}$,求$\dfrac{{A}_{1}M}{{A}_{1}{B}_{1}}$.
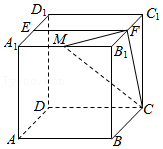 【答案详解】 【答案详解】 |
2021年高考数学北京18为加快新冠肺炎检测效率,某检测机构采取“$k$合1检测法”,即将$k$个人的拭子样本合并检测,若为阴性,则可确定所有样本都是阴性的,若为阳性,则还需要对本组的每个人再做检测.现有100人,已知其中2人感染病毒.
(1)①若采用“10合1检测法”,且两名患者在同一组,求总检测次数;
②已知10人分成一组,分10组,两名感染患者在同一组的概率为$\dfrac{1}{11}$,定义随机变量$X$为总检测次数,求检测次数$X$的分布列和数学期望$E(X)$;
(2)若采用“5合1检测法”,检测次数$Y$的期望为$E(Y)$,试比较$E(X)$和$E(Y)$的大小.(直接写出结果)【答案详解】 |
2021年高考数学北京19已知函数$f(x)=\dfrac{3-2x}{{x}^{2}+a}$.
(1)若$a=0$,求$y=f(x)$在$(1$,$f$(1)$)$处的切线方程;
(2)若函数$f(x)$在$x=-1$处取得极值,求$f(x)$的单调区间,以及最大值和最小值.【答案详解】 |
2021年高考数学北京20已知椭圆$E:\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1(a>b>0)$过点$A(0,-2)$,以四个顶点围成的四边形面积为$4\sqrt{5}$.
(1)求椭圆$E$的标准方程;
(2)过点$P(0,-3)$的直线$l$斜率为$k$,交椭圆$E$于不同的两点$B$,$C$,直线$AB$、$AC$交$y=-3$于点$M$、$N$,若$\vert PM\vert +\vert PN\vert \leqslant 15$,求$k$的取值范围.【答案详解】 |

