|
2021年高考数学北京16<-->2021年高考数学北京18
17.(13分)已知正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$,点$E$为$A_{1}D_{1}$中点,直线$B_{1}C_{1}$交平面$CDE$于点$F$.
(1)求证:点$F$为$B_{1}C_{1}$中点;
(2)若点$M$为棱$A_{1}B_{1}$上一点,且二面角$M-CF-E$的余弦值为$\dfrac{\sqrt{5}}{3}$,求$\dfrac{{A}_{1}M}{{A}_{1}{B}_{1}}$.
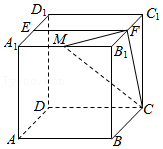
分析:(1)连结$DE$,利用线面平行的判定定理证明$CD//$平面$A_{1}B_{1}C_{1}D_{1}$,从而可证明$CD//EF$,即可证明四边形$A_{1}B_{1}FE$为平行四边形,四边形$EFC_{1}D_{1}$为平行四边形,可得$A_{1}E=B_{1}F$,$ED_{1}=FC_{1}$,即可证明$B_{1}F=FC_{1}$,故点$F$为$B_{1}C_{1}$的中点;
(2)建立合适的空间直角坐标系,设点$M(m$,0,$0)$,且$m<0$,求出所需点的坐标和向量的坐标,然后利用待定系数法求出平面$CMF$与$CDEF$的法向量,由向量的夹角公式列出关于$m$的关系式,求解即可得到答案.
(1)证明:

连结$DE$,
在正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中,$CD//C_{1}D_{1}$,$C_{1}D_{1}\subset$平面$A_{1}B_{1}C_{1}D_{1}$,$CD\not\subset$平面$A_{1}B_{1}C_{1}D_{1}$,
则$CD//$平面$A_{1}B_{1}C_{1}D_{1}$,因为平面$A_{1}B_{1}C_{1}D_{1}\bigcap$平面$CDEF=EF$,
所以$CD//EF$,则$EF//C_{1}D_{1}$,
故$A_{1}B_{1}//EF//C_{1}D_{1}$,又因为$A_{1}D_{1}//B_{1}C_{1}$,
所以四边形$A_{1}B_{1}FE$为平行四边形,四边形$EFC_{1}D_{1}$为平行四边形,
所以$A_{1}E=B_{1}F$,$ED_{1}=FC_{1}$,
而点$E$为$A_{1}D_{1}$的中点,所以$A_{1}E=ED_{1}$,
故$B_{1}F=FC_{1}$,则点$F$为$B_{1}C_{1}$的中点;
(2)解:以点$B_{1}$为原点,建立空间直角坐标系,如图所示,
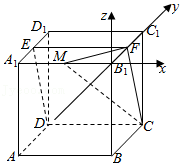
设正方体边长为2,设点$M(m$,0,$0)$,且$m<0$,
则$C(0$,2,$-2)$,$E(-2$,1,$0)$,$F(0$,1,$0)$,
故$\overrightarrow{FE}=(-2,0,0),\overrightarrow{FC}=(0,1,-2),\overrightarrow{FM}=(m,-1,0)$,
设平面$CMF$的法向量为$\overrightarrow{m}=(a,b,1)$,
则$\left\{\begin{array}{l}{\overrightarrow{m}\cdot \overrightarrow{FM}=0}\\ {\overrightarrow{m}\cdot \overrightarrow{FC}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{ma-b=0}\\ {b-2=0}\end{array}\right.$,
所以$a=\dfrac{2}{m}$,$b=2$,故$\overrightarrow{m}=(\dfrac{2}{m},2,1)$,
设平面$CDEF$的法向量为$\overrightarrow{n}=(x,y,1)$,
则$\left\{\begin{array}{l}{\overrightarrow{n}\cdot \overrightarrow{FE}=0}\\ {\overrightarrow{n}\cdot \overrightarrow{FC}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{-2x=0}\\ {y-2=0}\end{array}\right.$,
所以$x=0$,$y=2$,故$\overrightarrow{n}=(0,2,1)$,
因为二面角$M-CF-E$的余弦值为$\dfrac{\sqrt{5}}{3}$,
则$\vert \cos <\overrightarrow{m},\overrightarrow{n}>\vert =\dfrac{\vert \overrightarrow{m}\cdot \overrightarrow{n}\vert }{\vert \overrightarrow{m}\vert \vert \overrightarrow{n}\vert }=\dfrac{5}{\sqrt{\dfrac{4}{{m}^{2}}+4+1}\times \sqrt{{2}^{2}+1}}=\dfrac{\sqrt{5}}{3}$,
解得$m=\pm 1$,又$m<0$,
所以$m=-1$,
故$\dfrac{{A}_{1}M}{{A}_{1}{B}_{1}}=\dfrac{1}{2}$.
点评:本题考查了立体几何的综合应用,涉及了线面平行的性质定理的应用,二面角的应用,在求解有关空间角问题的时候,一般会建立合适的空间直角坐标系,将空间角问题转化为空间向量问题进行研究,属于中档题.
2021年高考数学北京16<-->2021年高考数学北京18
全网搜索"2021年高考数学北京17"相关
|

