2024年高考数学新高考Ⅱ-16(15分)已知函数$f(x)=e^{x}-ax-a^{3}$.
(1)当$a=1$时,求曲线$y=f(x)$在点$(1$,$f$(1)$)$处的切线方程;
(2)若$f(x)$有极小值,且极小值小于0,求$a$的取值范围.【答案详解】 |
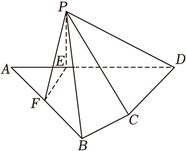
2024年高考数学新高考Ⅱ-17(15分)如图,平面四边形$ABCD$中,$AB=8$,$CD=3$,$AD=5\sqrt{3}$,$\angle ADC=90^\circ$,$\angle BAD=30^\circ$,点$E$,$F$满足$\overrightarrow{AE}=\dfrac{2}{5}\overrightarrow{AD}$,$\overrightarrow{AF}=\dfrac{1}{2}\overrightarrow{AB}$,将$\Delta AEF$沿$EF$对折至$\Delta PEF$,使得$PC=4\sqrt{3}$.
(1)证明:$EF\bot PD$;
(2)求面$PCD$与面$PBF$所成的二面角的正弦值.
 【答案详解】 【答案详解】 |
2024年高考数学新高考Ⅱ-18(17分)某投篮比赛分为两个阶段,每个参赛都由两名队员组成,比赛具体规则如下:第一阶段由参赛队中一名队员投篮3次,若3次都未投中,则该队被淘汰,比赛成员为0分,若至少投中一次,则该队进入第二阶段,由该队的另一名队员投篮3次,每次投中得5分,未投中得0分,该队的比赛成绩为第二阶段的得分总和.
某参赛队由甲、乙两名队员组成,设甲每次投中的概率为$p$,乙每次投中的概率为$q$,各次投中与否相互独立.
(1)若$p=0.4$,$q=0.5$,甲参加第一阶段比赛,求甲、乙所在队的比赛成绩不少于5分的概率;
(2)假设$0 < p < q$,
$(i)$为使得甲、乙所在队的比赛成绩为15分的概率最大,则该由谁参加第一阶段比赛?
$(ii)$为使得甲、乙所在队的比赛成绩的数学期望最大,应该由谁参加第一阶段比赛?【答案详解】 |
2024年高考数学新高考Ⅱ-19(17分)已知双曲线$C:x^{2}-y^{2}=m(m > 0)$,点$P_{1}(5,4)$在$C$上,$k$为常数,$0 < k < 1$,按照如下方式依次构造点$P_{n}(n=2$,3,$\dotsb )$,过$P_{n-1}$斜率为$k$的直线与$C$的左支交于点$Q_{n-1}$,令$P_{n}$为$Q_{n-1}$关于$y$轴的对称点,记$P_{n}$的坐标为$(x_{n}$,$y_{n})$.
(1)若$k=\dfrac{1}{2}$,求$x_{2}$,$y_{2}$;
(2)证明:数列$\{x_{n}-y_{n}\}$是公比为$\dfrac{1+k}{1-k}$的等比数列;
(3)设$S_{n}$为△$P_{n}P_{n+1}P_{n+2}$的面积,证明:对任意的正整数$n$,$S_{n}=S_{n+1}$.【答案详解】 |

