2024年高考数学上海春16(5分)现定义如下:当$x\in (n,n+1)$时$(n\in N)$,若$f(x+1)=f\prime (x)$,则称$f(x)$为延展函数.现有,当$x\in (0,1)$时,$g(x)=e^{x}$与$h(x)=x^{10}$均为延展函数,则以下结论$($ $)$
(1)存在$y=kx+b(k$,$b\in R$;$k$,$b\ne 0)$与$y=g(x)$有无穷个交点
(2)存在$y=kx+b(k$,$b\in R$;$k$,$b\ne 0)$与$y=h(x)$有无穷个交点
A.(1)(2)都成立 B.(1)(2)都不成立
C.(1)成立(2)不成立 D.(1)不成立(2)成立【答案详解】 |
2024年高考数学上海春17(14分)已知$f(x)=\sin (\omega x+\dfrac{\pi }{3})$,$\omega > 0$.
(1)设$\omega =1$,求解:$y=f(x)$,$x\in [0$,$\pi ]$的值域;
(2)$a > \pi (a\in R)$,$f(x)$的最小正周期为$\pi$,若在$x\in [\pi$,$a]$上恰有3个零点,求$a$的取值范围.【答案详解】 |
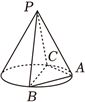
2024年高考数学上海春18(14分)如图,$PA$、$PB$、$PC$为圆锥三条母线,$AB=AC$.
(1)证明:$PA\bot BC$;
(2)若圆锥侧面积为$\sqrt{3}\pi ,BC$为底面直径,$BC=2$,求二面角$B-PA-C$的大小.
 【答案详解】 【答案详解】 |
2024年高考数学上海春19(14分)水果分为一级果和二级果,共136箱,其中一级果102箱,二级果34箱.
(1)随机挑选两箱水果,求恰好一级果和二级果各一箱的概率;
(2)进行分层抽样,共抽8箱水果,求一级果和二级果各几箱;
(3)抽取若干箱水果,其中一级果共120个,单果质量平均数为303.45克,方差为603.46;二级果48个,单果质量平均数为240.41克,方差为648.21;求168个水果的方差和平均数,并预估果园中单果的质量.【答案详解】 |
2024年高考数学上海春20(18分)在平面直角坐标系$xOy$中,已知点$A$为椭圆$\Gamma :\dfrac{{x}^{2}}{6}+\dfrac{{y}^{2}}{2}=1$上一点,$F_{1}$、$F_{2}$分别为椭圆的左、右焦点.
(1)若点$A$的横坐标为2,求$\vert AF_{1}\vert$的长;
(2)设$\Gamma$的上、下顶点分别为$M_{1}$、$M_{2}$,记△$AF_{1}F_{2}$的面积为$S_{1}$,△$AM_{1}M_{2}$的面积为$S_{2}$,若$S_{1}\geqslant S_{2}$,求$\vert OA\vert$的取值范围.
(3)若点$A$在$x$轴上方,设直线$AF_{2}$与$\Gamma$交于点$B$,与$y$轴交于点$K$,$KF_{1}$延长线与$\Gamma$交于点$C$,是否存在$x$轴上方的点$C$,使得$\overrightarrow{{F}_{1}A}+\overrightarrow{{F}_{1}B}+\overrightarrow{{F}_{1}C}=\lambda (\overrightarrow{{F}_{2}A}+\overrightarrow{{F}_{2}B}+\overrightarrow{{F}_{2}C})(\lambda \in R)$成立?若存在,请求出点$C$的坐标;若不存在,请说明理由.【答案详解】 |

