|
2024年高考数学上海春9<-->2024年高考数学上海春11
(5分)已知四棱柱$ABCD-A_{1}B_{1}C_{1}D_{1}$底面$ABCD$为平行四边形,$AA_{1}=3$,$BD=4$且$\overrightarrow{A{B}_{1}}\cdot \overrightarrow{BC}-\overrightarrow{A{D}_{1}}\cdot \overrightarrow{DC}=5$,求异面直线$AA_{1}$与$BD$的夹角 ____.
答案:$\arccos \dfrac{5}{12}$.
分析:由题将$\overrightarrow{A{B}_{1}}\cdot \overrightarrow{BC}-\overrightarrow{A{D}_{1}}\cdot \overrightarrow{DC}=5$转化为$\overrightarrow{AA_{1}}\cdot \overrightarrow{BD}=5$即可求解.
解:如图,
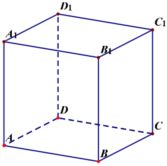
因为${\overrightarrow{AB}}_{1}=\overrightarrow{AB}+\overrightarrow{A{A}_{1}},\overrightarrow{A{D}_{1}}=\overrightarrow{AD}+\overrightarrow{A{A}_{1}}$,又$\overrightarrow{A{B}_{1}}\cdot \overrightarrow{BC}-\overrightarrow{A{D}_{1}}\cdot \overrightarrow{DC}=5$,
$\therefore$$(\overrightarrow{AB}+\overrightarrow{A{A}_{1}})\cdot \overrightarrow{AD}-(\overrightarrow{AD}+\overrightarrow{A{A}_{1}})\cdot \overrightarrow{DC}=5$,
化简得$\overrightarrow{AA_{1}}\cdot \overrightarrow{BD}=5$,
$\therefore$$\overrightarrow{A{A}_{1}}\cdot \overrightarrow{BD}=3\times 4\times \cos \theta =5$,
$\therefore$$\cos \theta =\dfrac{5}{12}$.
异面直线$AA_{1}$与$BD$的夹角为$\arccos \dfrac{5}{12}$.
点评:本题考查向量法求立体几何中的线线角,属于中档题.
2024年高考数学上海春9<-->2024年高考数学上海春11
全网搜索"2024年高考数学上海春10"相关
|

