| 2021年高考数学甲卷-文16已知$F_{1}$,$F_{2}$为椭圆$C:\dfrac{{x}^{2}}{16}+\dfrac{{y}^{2}}{4}=1$的两个焦点,$P$,$Q$为$C$上关于坐标原点对称的两点,且$\vert PQ\vert =\vert F_{1}F_{2}\vert$,则四边形$PF_{1}QF_{2}$的面积为____.【答案详解】 |
2021年高考数学甲卷-文17(12分)甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:
| | 一级品 | 二级品 |
合计 | | 甲机床 | 150 | 50 | 200 | | 乙机床 | 120 | 80 | 200 | | 合计 | 270 | 130 | 400 |
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?
(2)能否有$99%$的把握认为甲机床的产品质量与乙机床的产品质量有差异?
附:$K^{2}=\dfrac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| $P(K^{2}\geqslant k)$ | 0.050 | 0.010 | 0.001 | | $k$ | 3.841 | 6.635 | 10.828 |
【答案详解】 |
| 2021年高考数学甲卷-文18(12分)记$S_{n}$为数列$\{a_{n}\}$的前$n$项和,已知$a_{n}>0$,$a_{2}=3a_{1}$,且数列$\{\sqrt{{S}_{n}}\}$是等差数列,证明:$\{a_{n}\}$是等差数列.【答案详解】 |
2021年高考数学甲卷-文19(12分)已知直三棱柱$ABC-A_{1}B_{1}C_{1}$中,侧面$AA_{1}B_{1}B$为正方形,$AB=BC=2$,$E$,$F$分别为$AC$和$CC_{1}$的中点,$BF\bot A_{1}B_{1}$.
(1)求三棱锥$F-EBC$的体积;
(2)已知$D$为棱$A_{1}B_{1}$上的点,证明:$BF\bot DE$.
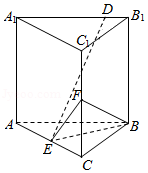 【答案详解】 【答案详解】 |
2021年高考数学甲卷-文20设函数$f(x)=a^{2}x^{2}+ax-3lnx+1$,其中$a>0$.
(1)讨论$f(x)$的单调性;
(2)若$y=f(x)$的图像与$x$轴没有公共点,求$a$的取值范围.【答案详解】 |

