|
2021年高考数学甲卷-文22<-->返回列表
[选修4-5:不等式选讲](10分)
23.已知函数$f(x)=\vert x-2\vert$,$g(x)=\vert 2x+3\vert -\vert 2x-1\vert$.
(1)画出$y=f(x)$和$y=g(x)$的图像;
(2)若$f(x+a)\geqslant g(x)$,求$a$的取值范围.
分析:(1)通过对$x$分类讨论,写出分段函数的形式,画出图像即可得出.
(2)由图像可得:$f$(6)$=4$,$g(\dfrac{1}{2})=4$,若$f(x+a)\geqslant g(x)$,说明把函数$f(x)$的图像向左或向右平移$\vert a\vert$单位以后,$f(x)$的图像不在$g(x)$的下方,由图像观察可得出结论.
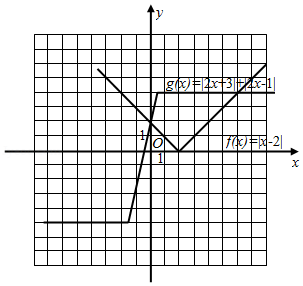
解:(1)函数$f(x)=\vert x-2\vert =\left\{\begin{array}{l}{x-2,x\geqslant 2}\\ {2-x,x<2}\end{array}\right.$,
$g(x)=\vert 2x+3\vert -\vert 2x-1\vert =\left\{\begin{array}{l}{4,x\geqslant \dfrac{1}{2}}\\ {4x+2,-\dfrac{3}{2}<x<\dfrac{1}{2}}\\ {-4,x\leqslant -\dfrac{3}{2}}\end{array}\right.$.
画出$y=f(x)$和$y=g(x)$的图像;
(2)由图像可得:$f$(6)$=4$,$g(\dfrac{1}{2})=4$,
若$f(x+a)\geqslant g(x)$,说明把函数$f(x)$的图像向左或向右平移$\vert a\vert$单位以后,$f(x)$的图像不在$g(x)$的下方,
由图像观察可得:$a\geqslant 2-\dfrac{1}{2}+4=\dfrac{11}{2}$
$\therefore a$的取值范围为$[\dfrac{11}{2}$,$+\infty )$.
点评:本题考查了分段函数的图像与性质、方程与不等式的解法,考查了推理能力与计算能力,属于中档题.
2021年高考数学甲卷-文22<-->返回列表
全网搜索"2021年高考数学甲卷-文23"相关
|

