| 2024年高考数学甲卷-文16(5分)曲线$y=x^{3}-3x$与$y=-(x-1)^{2}+a$在$(0,+\infty )$上有两个不同的交点,则$a$的取值范围为____.【答案详解】 |
2024年高考数学甲卷-文17(12分)已知等比数列$\{a_{n}\}$的前$n$项和为$S_{n}$,且$2S_{n}=3a_{n+1}-3$.
(1)求$\{a_{n}\}$的通项公式;
(2)求数列$\{S_{n}\}$的通项公式.【答案详解】 |
2024年高考数学甲卷-文18(12分)某工厂进行生产线智能化升级改造.升级改造后,从该工厂甲、乙两个车间的产品中随机抽取150件进行检验,数据如下:
| | 优级品 | 合格品 | 不合格品 |
总计 | | 甲车间 | 26 | 24 | 0 | 50 | | 乙车间 | 70 | 28 | 2 | 100 | | 总计 | 96 | 52 | 2 | 150 | (1)填写如下列联表:
能否有$95%$的把握认为甲、乙两车间产品的优级品率存在差异?能否有$99%$的把握认为甲、乙两车间产品的优级品率存在差异?
(2)已知升级改造前该工厂产品的优级品率$p=0.5$.设$\overline{p}$为升级改造后抽取的$n$件产品的优级品率.如果$\overline{p} > p+1.65\sqrt{\dfrac{p(1-p)}{n}}$,则认为该工厂产品的优级品率提高了.根据抽取的150件产品的数据,能否认为生产线智能化升级改造后,该工厂产品的优级品率提高了?$(\sqrt{150}\approx 12.247)$
附:$K^{2}=\dfrac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,
| $P(K^{2}\geqslant k)$ |
0.050 | 0.010 | 0.001 | | $k$ | 3.841 | 6.635 | 10.828 |
【答案详解】 |
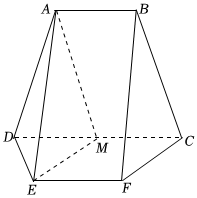
2024年高考数学甲卷-文19(12分)如图,在以$A$,$B$,$C$,$D$,$E$,$F$为顶点的五面体中,四边形$ABCD$与四边形$ADEF$均为等腰梯形,$AB//CD$,$CD//EF$,$AB=DE=EF=CF=2$,$CD=4$,$AD=BC=\sqrt{10}$,$AE=2\sqrt{3}$,$M$为$CD$的中点.
(1)证明:$EM//$平面$BCF$;
(2)求点$M$到$ADE$的距离.
 【答案详解】 【答案详解】 |
2024年高考数学甲卷-文20(12分)已知函数$f(x)=a(x-1)-\ln x+1$.
(1)求$f(x)$的单调区间;
(2)若$a\leqslant 2$时,证明:当$x > 1$时,$f(x) < e^{x-1}$恒成立.【答案详解】 |

