|
2024年高考数学甲卷-文7<-->2024年高考数学甲卷-文9
(5分)函数$f(x)=-x^{2}+(e^{x}-e^{-x})\sin x$ 的区间$[-2.8$,$2.8]$的图像大致为( )
A.
B.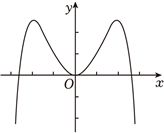
C.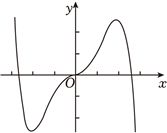
D.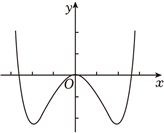
答案:B
分析:先结合偶函数的性质,判断$AC$,再结合特殊值,即可求解.
解:$f(x)=-x^{2}+(e^{x}-e^{-x})\sin x$,
则$f(-x)=-(-x)^{2}+(e^{-x}-e^{x})\sin (-x)=-x^{2}+(e^{x}-e^{-x})\sin x=f(x)$,
故$f(x)$为偶函数,故$AC$错误;
$f$(1)$=-1+(e^{1}-e^{-1})\sin 1 > -1+(e-\dfrac{1}{e})\sin \dfrac{\pi }{6}=\dfrac{e}{2}-1-\dfrac{1}{2e} > \dfrac{1}{4}-\dfrac{1}{2e} > 0$,故$D$错误,$B$正确.
故选:B.
点评:本题主要考查函数图象的应用,属于基础题.
2024年高考数学甲卷-文7<-->2024年高考数学甲卷-文9
全网搜索"2024年高考数学甲卷-文8"相关
|

