2021年上海

面向未来，活在当下！

收藏夹
我的

当前：首页 > 数学 > 高考题 > 2021 > 2021年上海

2021年高考数学上海1已知

$z_{1}=1+i$ ，

$z_{2}=2+3i$ ，求

$z_{1}+z_{2}=$ ____．【答案详解】

2021年高考数学上海2已知

$A=\{x\vert 2x\leqslant 1\}$ ，

$B=\{-1$ ，0，

$1\}$ ，则

$A\bigcap B=$ ____．【答案详解】

2021年高考数学上海3若

$x^{2}+y^{2}-2x-4y=0$ ，求圆心坐标为____．【答案详解】

2021年高考数学上海4如图正方形

$ABCD$ 的边长为3，求

$\overrightarrow{AB}\cdot \overrightarrow{AC}=$ ____．

【答案详解】

2021年高考数学上海5已知

$f(x)=\dfrac{3}{x}+2$ ，则

$f^{-1}$ （1）

$=$ ____．【答案详解】

2021年高考数学上海6已知二项式

$(x+a)^{5}$ 展开式中，

$x^{2}$ 的系数为80，则

$a=$ ____．【答案详解】

2021年高考数学上海7已知

$\left\{\begin{array}{l}{x\leqslant 3}\\ {2x-y-2\geqslant 0}\\ {3x+y-8\geqslant 0}\end{array}\right.$ ，

$z=x-y$ ，则

$z$ 的最大值为____．【答案详解】

2021年高考数学上海8已知

$\{a_{n}\}$ 为无穷等比数列，

$a_{1}=3$ ，

$a_{n}$ 的各项和为9，

$b_{n}=a_{2n}$ ，则数列

$\{b_{n}\}$ 的各项和为____．【答案详解】

2021年高考数学上海9已知圆柱的底面圆半径为1，高为2，

$AB$ 为上底面圆的一条直径，

$C$ 是下底面圆周上的一个动点，则

$ABC$ 的面积的取值范围为 ____．【答案详解】

2021年高考数学上海10知花博会有四个不同的场馆

$A$ ，

$B$ ，

$C$ ，

$D$ ，甲、乙两人每人选2个去参观，则他们的选择中，恰有一个馆相同的概率为____．【答案详解】

2021年高考数学上海11已知抛物线

$y^{2}=2px(p>0)$ ，若第一象限的

$A$ ，

$B$ 在抛物线上，焦点为

$F$ ，

$\vert AF\vert =2$ ，

$\vert BF\vert =4$ ，

$\vert AB\vert =3$ ，求直线

$AB$ 的斜率为 ____．【答案详解】

2021年高考数学上海12已知

$a_{i}\in N*(i=1$ ，2，

$\ldots$ ，

$9)$ 对任意的

$k\in N*(2\leqslant k\leqslant 8)$ ，

$a_{k}=a_{k-1}+1$ 或

$a_{k}=a_{k+1}-1$ 中有且仅有一个成立，

$a_{1}=6$ ，

$a_{9}=9$ ，则

$a_{1}+\ldots +a_{9}$ 的最小值为____．【答案详解】

2021年高考数学上海13以下哪个函数既是奇函数，又是减函数(　　)
A．

$y=-3x$ B．

$y=x^{3}$ C．

$y=\log _{3}x$ D．

$y=3^{x}$ 【答案详解】

2021年高考数学上海14已知参数方程

$\left\{\begin{array}{l}{x=3t-4{t}^{3}}\\ {y=2t\sqrt{1-{t}^{2}}}\end{array}\right.$ ，

$t\in [-1$ ，

$1]$ ，以下哪个图符合该方程(　　)
A．

B．

C．

D．

【答案详解】

2021年高考数学上海15已知

$f(x)=3\sin x+2$ ，对任意的

$x_{1}\in [0$ ，

$\dfrac{\pi }{2}]$ ，都存在

$x_{2}\in [0$ ，

$\dfrac{\pi }{2}]$ ，使得

$f(x_{1})=2f(x_{2}+\theta )+2$ 成立，则下列选项中，

$\theta$ 可能的值是(　　)
A．

$\dfrac{3\pi }{5}$ B．

$\dfrac{4\pi }{5}$ C．

$\dfrac{6\pi }{5}$ D．

$\dfrac{7\pi }{5}$ 【答案详解】

2021年高考数学上海16已知

$x_{1}$ ，

$y_{1}$ ，

$x_{2}$ ，

$y_{2}$ ，

$x_{3}$ ，

$y_{3}$ ，同时满足①$x_{1} A．$2x_{2} B．

$2x_{2}>x_{1}+x_{3}$
C．$x_{2}^{2} D．

$x_{2}^{2}>x_{1}x_{3}$ 【答案详解】

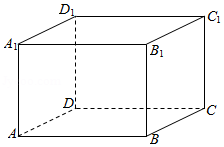
2021年高考数学上海17如图，在长方体

$ABCD-A_{1}B_{1}C_{1}D_{1}$ 中，已知

$AB=BC=2$ ，

$AA_{1}=3$ ．
（1）若

$P$ 是棱

$A_{1}D_{1}$ 上的动点，求三棱锥

$C-PAD$ 的体积；
（2）求直线

$AB_{1}$ 与平面

$ACC_{1}A_{1}$ 的夹角大小．

【答案详解】

2021年高考数学上海18在

$\Delta ABC$ 中，已知

$a=3$ ，

$b=2c$ ．
（1）若

$A=\dfrac{2\pi }{3}$ ，求

$S_{\Delta ABC}$ ．
（2）若

$2\sin B-\sin C=1$ ，求

$C_{\Delta ABC}$ ．【答案详解】

2021年高考数学上海19已知一企业今年第一季度的营业额为1.1亿元，往后每个季度增加0.05亿元，第一季度的利润为0.16亿元，往后每一季度比前一季度增长

$4%$ ．
（1）求今年起的前20个季度的总营业额；
（2）请问哪一季度的利润首次超过该季度营业额的

$18%$ ？【答案详解】

2021年高考数学上海20已知

$\Gamma :\dfrac{{x}^{2}}{2}+y^{2}=1$ ，

$F_{1}$ ，

$F_{2}$ 是其左、右交焦点，直线

$l$ 过点

$P(m$ ，

$0)(m\leqslant -\sqrt{2})$ ，交椭圆于

$A$ ，

$B$ 两点，且

$A$ ，

$B$ 在

$x$ 轴上方，点

$A$ 在线段

$BP$ 上．
（1）若

$B$ 是上顶点，

$\vert \overrightarrow{B{F}_{1}}\vert =\vert \overrightarrow{P{F}_{1}}\vert$ ，求

$m$ 的值；
（2）若

$\overrightarrow{{F}_{1}A}\cdot \overrightarrow{{F}_{2}A}=\dfrac{1}{3}$ ，且原点

$O$ 到直线

$l$ 的距离为

$\dfrac{4\sqrt{15}}{15}$ ，求直线

$l$ 的方程；
（3）证明：对于任意

$m<-\sqrt{2}$ ，使得

$\overrightarrow{{F}_{1}A}//\overrightarrow{{F}_{2}B}$ 的直线有且仅有一条．【答案详解】

2021年高考数学上海21已知

$x_{1}$ ，

$x_{2}\in R$ ，若对任意的

$x_{2}-x_{1}\in S$ ，

$f(x_{2})-f(x_{1})\in S$ ，则有定义：

$f(x)$ 是在

$S$ 关联的．
（1）判断和证明

$f(x)=2x-1$ 是否在

$[0$ ，

$+\infty )$ 关联？是否有

$[0$ ，

$1]$ 关联？
（2）若

$f(x)$ 是在

$\{3\}$ 关联的，

$f(x)$ 在

$x\in [0$ ，

$3)$ 时，

$f(x)=x^{2}-2x$ ，求解不等式：

$2\leqslant f(x)\leqslant 3$ ．
（3）证明：

$f(x)$ 是

$\{1\}$ 关联的，且是在

$[0$ ，

$+\infty )$ 关联的，当且仅当“

$f(x)$ 在

$[1$ ，

$2]$ 是关联的”．【答案详解】

开心教练从2004年开始自费开设这个网站. 为了可以持续免费提供这些内容, 并且没有广告干扰，请大家随意打赏，谢谢！,
（微信中可直接长按微信打赏二维码。）

微信	支付宝