| 2022年高考数学乙卷-文16(5分)若$f(x)=\ln \vert a+\dfrac{1}{1-x}\vert +b$是奇函数,则$a=$____,$b=$____.【答案详解】 |
2022年高考数学乙卷-文17(12分)记$\Delta ABC$的内角$A$,$B$,$C$的对边分别为$a$,$b$,$c$,已知$\sin C\sin (A-B)=\sin B\sin (C-A)$.
(1)若$A=2B$,求$C$;
(2)证明:$2a^{2}=b^{2}+c^{2}$.【答案详解】 |
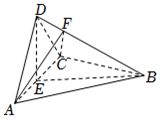
2022年高考数学乙卷-文18(12分)如图,四面体$ABCD$中,$AD\bot CD$,$AD=CD$,$\angle ADB=\angle BDC$,$E$为$AC$的中点.
(1)证明:平面$BED\bot$平面$ACD$;
(2)设$AB=BD=2$,$\angle ACB=60^\circ$,点$F$在$BD$上,当$\Delta AFC$的面积最小时,求三棱锥$F-ABC$的体积.
 【答案详解】 【答案详解】 |
2022年高考数学乙卷-文19(12分)某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位:$m^{2})$和材积量(单位:$m^{3})$,得到如下数据:
| 样本号$i$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 总和 | | 根部横截面积$x_{i}$ | 0.04 | 0.06 | 0.04 | 0.08 | 0.08 | 0.05 | 0.05 | 0.07 | 0.07 | 0.06 | 0.6 | | 材积量$y_{i}$ | 0.25 | 0.40 | 0.22 | 0.54 | 0.51 | 0.34 | 0.36 | 0.46 | 0.42 | 0.40 | 3.9 |
并计算得$\sum\limits_{i=1}^{10}x_{i}^{2}=0.038$,$\sum\limits_{i=1}^{10}y_{i}^{2}=1.6158$,$\sum\limits_{i=1}^{10}x_{i}y_{i}=0.2474$.
(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量;
(2)求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到$0.01)$;
(3)现测量了该林区所有这种树木的根部横截面积,并得到所有这种树木的根部横截面积总和为$186m^{2}$.已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材积量的估计值.
附:相关系数$r=\dfrac{\sum\limits_{i=1}^n{({{x_i}-\overline{x}})}({{y_i}-\overline{y}})}{\sqrt{\sum\limits_{i=1}^n{{({{x_i}-\overline{x}})}^2}\sum\limits_{i=1}^n{{({{y_i}-\overline{y}})}^2}}}$,$\sqrt{1.896}\approx 1.377$.【答案详解】 |
2022年高考数学乙卷-文20(12分)已知函数$f(x)=ax-\dfrac{1}{x}-(a+1)\ln x$.
(1)当$a=0$时,求$f(x)$的最大值;
(2)若$f(x)$恰有一个零点,求$a$的取值范围.【答案详解】 |

