2022年浙江

面向未来，活在当下！

收藏夹
我的

当前：首页 > 数学 > 高考题 > 2022 > 2022年浙江

2022年高考数学浙江1（4分）设集合

$A=\{1，2\}$ ，

$B=\{2，4，6\}$ ，则

$A\bigcup B=$ (　　)
A．

$\{2\}$ B．

$\{1，2\}$ C．

$\{2，4，6\}$ D．

$\{1，2，4，6\}$ 【答案详解】

2022年高考数学浙江2（4分）已知

$a$ ，

$b\in R$ ，

$a+3i=(b+i)i(i$ 为虚数单位），则(　　)
A．

$a=1$ ，

$b=-3$ B．

$a=-1$ ，

$b=3$ C．

$a=-1$ ，

$b=-3$ D．

$a=1$ ，

$b=3$ 【答案详解】

2022年高考数学浙江3（4分）若实数

$x$ ，

$y$ 满足约束条件

$\left\{\begin{array}{l}x-2\geqslant 0,\\ 2x+y-7\leqslant 0,\\ x-y-2\leqslant 0,\end{array}\right.$ 则

$z=3x+4y$ 的最大值是(　　)
A．20 B．18 C．13 D．6【答案详解】

2022年高考数学浙江4（4分）设

$x\in R$ ，则“

$\sin x=1$ ”是“

$\cos x=0$ ”的(　　)
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件【答案详解】

2022年高考数学浙江5（4分）某几何体的三视图如图所示（单位：

$cm)$ ，则该几何体的体积（单位：

$cm^{3})$ 是(　　)

A．

$22\pi$ B．

$8\pi$ C．

$\dfrac{22}{3}\pi$ D．

$\dfrac{16}{3}\pi$ 【答案详解】

2022年高考数学浙江6（4分）为了得到函数

$y=2\sin 3x$ 的图象，只要把函数

$y=2\sin (3x+\dfrac{\pi }{5})$ 图象上所有的点(　　)
A．向左平移

$\dfrac{\pi }{5}$ 个单位长度 B．向右平移

$\dfrac{\pi }{5}$ 个单位长度
C．向左平移

$\dfrac{\pi }{15}$ 个单位长度 D．向右平移

$\dfrac{\pi }{15}$ 个单位长度【答案详解】

2022年高考数学浙江7（4分）已知

$2^{a}=5$ ，

$\log _{8}3=b$ ，则

$4^{a-3b}=($ 　　)
A．25 B．5 C．

$\dfrac{25}{9}$ D．

$\dfrac{5}{3}$ 【答案详解】

2022年高考数学浙江8（4分）如图，已知正三棱柱

$ABC-A_{1}B_{1}C_{1}$ ，

$AC=AA_{1}$ ，

$E$ ，

$F$ 分别是棱

$BC$ ，

$A_{1}C_{1}$ 上的点．记

$EF$ 与

$AA_{1}$ 所成的角为

$\alpha$ ，

$EF$ 与平面

$ABC$ 所成的角为

$\beta$ ，二面角

$F-BC-A$ 的平面角为

$\gamma$ ，则(　　)

A．

$\alpha \leqslant \beta \leqslant \gamma$ B．

$\beta \leqslant \alpha \leqslant \gamma$ C．

$\beta \leqslant \gamma \leqslant \alpha$ D．

$\alpha \leqslant \gamma \leqslant \beta$ 【答案详解】

2022年高考数学浙江9（4分）已知

$a$ ，

$b\in R$ ，若对任意

$x\in R$ ，

$a\vert x-b\vert +\vert x-4\vert -\vert 2x-5\vert \geqslant 0$ ，则(　　)
A．

$a\leqslant 1$ ，

$b\geqslant 3$ B．

$a\leqslant 1$ ，

$b\leqslant 3$ C．

$a\geqslant 1$ ，

$b\geqslant 3$ D．

$a\geqslant 1$ ，

$b\leqslant 3$ 【答案详解】

2022年高考数学浙江10（4分）已知数列

$\{a_{n}\}$ 满足

$a_{1}=1$ ，

$a_{n+1}=a_{n}-\dfrac{1}{3}a_{n}^{2}(n\in N^{*})$ ，则(　　)
A．

$2 < 100a_{100} < \dfrac{5}{2}$ B．

$\dfrac{5}{2} < 100a_{100} < 3$ C．

$3 < 100a_{100} < \dfrac{7}{2}$ D．

$\dfrac{7}{2} < 100a_{100} < 4$ 【答案详解】

2022年高考数学浙江11（4分）我国南宋著名数学家秦九韶，发现了从三角形三边求面积的公式，他把这种方法称为“三斜求积”，它填补了我国传统数学的一个空白．如果把这个方法写成公式，就是

$S=\sqrt{\dfrac{1}{4}[{{c^2}{a^2}-{{({\dfrac{{c^2}+{a^2}-{b^2}}{2}})}^2}}]}$ ，其中

$a$ ，

$b$ ，

$c$ 是三角形的三边，

$S$ 是三角形的面积．设某三角形的三边

$a=\sqrt{2}$ ，

$b=\sqrt{3}$ ，

$c=2$ ，则该三角形的面积

$S=$ ____．【答案详解】

2022年高考数学浙江12（6分）已知多项式

$(x+2)(x-1)^{4}=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}+a_{5}x^{5}$ ，则

$a_{2}=$ 　____，

$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}=$ ____．【答案详解】

2022年高考数学浙江13（6分）若

$3\sin \alpha -\sin \beta =\sqrt{10}$ ，

$\alpha +\beta =\dfrac{\pi }{2}$ ，则

$\sin \alpha =$ ____，

$\cos 2\beta =$ ____．【答案详解】

2022年高考数学浙江14（6分）已知函数

$f(x)=\left\{\begin{array}{l}{-{x^2}+2,x\leqslant 1,}\\ {x+\dfrac{1}{x}-1,x > 1,}\end{array}\right.$ 则

$f(f(\dfrac{1}{2}))=$ ____；若当

$x\in [a$ ，

$b]$ 时，

$1\leqslant f(x)\leqslant 3$ ，则

$b-a$ 的最大值是____．【答案详解】

2022年高考数学浙江15（6分）现有7张卡片，分别写上数字1，2，2，3，4，5，6．从这7张卡片中随机抽取3张，记所抽取卡片上数字的最小值为

$\xi$ ，则

$P(\xi =2)=$ ____，

$E(\xi )=$ ____．【答案详解】

2022年高考数学浙江16（4分）已知双曲线

$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a > 0,b > 0)$ 的左焦点为

$F$ ，过

$F$ 且斜率为

$\dfrac{b}{4a}$ 的直线交双曲线于点

$A(x_{1}$ ，

$y_{1})$ ，交双曲线的渐近线于点

$B(x_{2}$ ，

$y_{2})$ 且

$x_{1} < 0 < x_{2}$ ．若

$\vert FB\vert =3\vert FA\vert$ ，则双曲线的离心率是____．【答案详解】

2022年高考数学浙江17（4分）设点

$P$ 在单位圆的内接正八边形

$A_{1}A_{2}\ldots A_{8}$ 的边

$A_{1}A_{2}$ 上，则

$\overrightarrow{P{A}_{1}}^{2}+\overrightarrow{P{A}_{2}}^{2}+\ldots +\overrightarrow{P{A}_{8}}^{2}$ 的取值范围是____．【答案详解】

2022年高考数学浙江18（14分）在

$\Delta ABC$ 中，角

$A$ ，

$B$ ，

$C$ 所对的边分别为

$a$ ，

$b$ ，

$c$ ．已知

$4a=\sqrt{5}c$ ，

$\cos C=\dfrac{3}{5}$ ．
（Ⅰ）求

$\sin A$ 的值；
（Ⅱ）若

$b=11$ ，求

$\Delta ABC$ 的面积．【答案详解】

2022年高考数学浙江19（15分）如图，已知

$ABCD$ 和

$CDEF$ 都是直角梯形，

$AB//DC$ ，

$DC//EF$ ，

$AB=5$ ，

$DC=3$ ，

$EF=1$ ，

$\angle BAD=\angle CDE=60^\circ$ ，二面角

$F-DC-B$ 的平面角为

$60^\circ$ ．设

$M$ ，

$N$ 分别为

$AE$ ，

$BC$ 的中点．
（Ⅰ）证明：

$FN\bot AD$ ；
（Ⅱ）求直线

$BM$ 与平面

$ADE$ 所成角的正弦值．

【答案详解】

2022年高考数学浙江20（15分）已知等差数列

$\{a_{n}\}$ 的首项

$a_{1}=-1$ ，公差

$d > 1$ ．记

$\{a_{n}\}$ 的前

$n$ 项和为

$S_{n}(n\in N^{*})$ ．
（Ⅰ）若

$S_{4}-2a_{2}a_{3}+6=0$ ，求

$S_{n}$ ；
（Ⅱ）若对于每个

$n\in N^{*}$ ，存在实数

$c_{n}$ ，使

$a_{n}+c_{n}$ ，

$a_{n+1}+4c_{n}$ ，

$a_{n+2}+15c_{n}$ 成等比数列，求

$d$ 的取值范围．【答案详解】

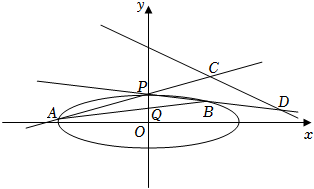
2022年高考数学浙江21（15分）如图，已知椭圆

$\dfrac{x^2}{12}+y^{2}=1$ ．设

$A$ ，

$B$ 是椭圆上异于

$P(0,1)$ 的两点，且点

$Q(0,\dfrac{1}{2})$ 在线段

$AB$ 上，直线

$PA$ ，

$PB$ 分别交直线

$y=-\dfrac{1}{2}x+3$ 于

$C$ ，

$D$ 两点．
（Ⅰ）求点

$P$ 到椭圆上点的距离的最大值；
（Ⅱ）求

$\vert CD\vert$ 的最小值．

【答案详解】

2022年高考数学浙江22（15分）设函数

$f(x)=\dfrac{e}{2x}+\ln x(x > 0)$ ．
（Ⅰ）求

$f(x)$ 的单调区间；
（Ⅱ）已知

$a$ ，

$b\in R$ ，曲线

$y=f(x)$ 上不同的三点

$(x_{1}$ ，

$f(x_{1}))$ ，

$(x_{2}$ ，

$f(x_{2}))$ ，

$(x_{3}$ ，

$f(x_{3}))$ 处的切线都经过点

$(a,b)$ ．证明：
（ⅰ）若

$a > e$ ，则

$0 < b-f$ （a）

$< \dfrac{1}{2}(\dfrac{a}{e}-1)$ ；
（ⅱ）若

$0 < a < e$ ，

$x_{1} < x_{2} < x_{3}$ ，则

$\dfrac{2}{e}+\dfrac{e-a}{6{e^2}} < \dfrac{1}{x_1}+\dfrac{1}{x_3} < \dfrac{2}{a}-\dfrac{e-a}{6{e^2}}$ ．
（注

$:e=2.71828\ldots$ 是自然对数的底数）【答案详解】

开心教练从2004年开始自费开设这个网站. 为了可以持续免费提供这些内容, 并且没有广告干扰，请大家随意打赏，谢谢！,
（微信中可直接长按微信打赏二维码。）

微信	支付宝