|
2022年高考数学浙江20<-->2022年高考数学浙江22
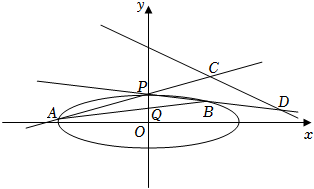
(15分)如图,已知椭圆$\dfrac{x^2}{12}+y^{2}=1$.设$A$,$B$是椭圆上异于$P(0,1)$的两点,且点$Q(0,\dfrac{1}{2})$在线段$AB$上,直线$PA$,$PB$分别交直线$y=-\dfrac{1}{2}x+3$于$C$,$D$两点.
(Ⅰ)求点$P$到椭圆上点的距离的最大值;
(Ⅱ)求$\vert CD\vert$的最小值.
分析:(Ⅰ)设椭圆上任意一点$M(x,y)$,利用两点间的距离公式结合二次函数的性质即可得解;
(Ⅱ)设直线$AB$方程并与椭圆方程联立,利用韦达定理得到两根之和与两根之积,进而表示出$\vert x_{1}-x_{2}\vert$,再分别联立直线$AP$,直线$BP$与直线$y=-\dfrac{1}{2}x+3$,得到$C$,$D$两点的坐标,由此可表示出$\vert CD\vert$,再转化求解即可.
解:(Ⅰ)设椭圆上任意一点$M(x,y)$,则$\vert PM\vert ^{2}=x^{2}+(y-1)^{2}=12-12y^{2}+y^{2}-2y+1=-11y^{2}-2y+13$,$y\in [-1$,$1]$,
而函数$z=-11y^{2}-2y+13$的对称轴为$y=-\dfrac{1}{11}\in [-1,1]$,则其最大值为$-11\times (-\dfrac{1}{11})^{2}+2\times \dfrac{1}{11}+13=\dfrac{144}{11}$,
$\therefore$$\vert PM{\vert }_{max}=\sqrt{\dfrac{144}{11}}=\dfrac{12\sqrt{11}}{11}$,即点$P$到椭圆上点的距离的最大值为$\dfrac{12\sqrt{11}}{11}$;
(Ⅱ)设直线$AB:y=kx+\dfrac{1}{2},A({x}_{1},{y}_{1}),B({x}_{2},{y}_{2})$,
联立直线$AB$与椭圆方程有$\left\{\begin{array}{l}{y=kx+\dfrac{1}{2}}\\ {\dfrac{{x}^{2}}{12}+{y}^{2}=1}\end{array}\right.$,消去$y$并整理可得,$(12k^{2}+1)x^{2}+12kx-9=0$,
由韦达定理可得,${x}_{1}+{x}_{2}=-\dfrac{12k}{12{k}^{2}+1},{x}_{1}{x}_{2}=-\dfrac{9}{12{k}^{2}+1}$,
$\therefore$$\vert {x}_{1}-{x}_{2}\vert =\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}=\sqrt{(-\dfrac{12k}{12{k}^{2}+1})^{2}+\dfrac{36}{12{k}^{2}+1}}=\dfrac{6\sqrt{16{k}^{2}+1}}{12{k}^{2}+1}$,
设$C(x_{3}$,$y_{3})$,$D(x_{4}$,$y_{4})$,直线$AP:y=\dfrac{{y}_{1}-1}{{x}_{1}}x+1$,直线$BP:y=\dfrac{{y}_{2}-1}{{x}_{2}}x+1$,
联立$\left\{\begin{array}{l}{y=\dfrac{{y}_{1}-1}{{x}_{1}}x+1}\\ {y=-\dfrac{1}{2}x+3}\end{array}\right.$以及$\left\{\begin{array}{l}{y=\dfrac{{y}_{2}-1}{{x}_{2}}x+1}\\ {y=-\dfrac{1}{2}x+3}\end{array}\right.$,
可得${x}_{3}=\dfrac{4{x}_{1}}{(2k+1){x}_{1}-1},{x}_{4}=\dfrac{4{x}_{2}}{(2k+1){x}_{2}-1}$,
$\therefore$由弦长公式可得$\vert CD\vert =\sqrt{1+(-\dfrac{1}{2})^{2}}\vert {x}_{3}-{x}_{4}\vert =\dfrac{\sqrt{5}}{2}\vert \dfrac{4{x}_{1}}{(2k+1){x}_{1}-1}-\dfrac{4{x}_{2}}{(2k+1){x}_{2}-1}\vert$
$=2\sqrt{5}\vert \dfrac{{x}_{1}-{x}_{2}}{[(2k+1){x}_{1}-1][(2k+1){x}_{2}-1]}\vert =2\sqrt{5}\vert \dfrac{{x}_{1}-{x}_{2}}{(2k+1)^{2}{x}_{1}{x}_{2}-(2k+1)({x}_{1}+{x}_{2})+1}\vert$
$=\dfrac{3\sqrt{5}}{2}\vert \dfrac{\sqrt{16{k}^{2}+1}}{3k+1}\vert =\dfrac{6\sqrt{5}}{5}\cdot \dfrac{\sqrt{16{k}^{2}+1}\cdot \sqrt{\dfrac{9}{16}+1}}{\vert 3k+1\vert }\geqslant \dfrac{6\sqrt{5}}{5}\times \dfrac{\sqrt{(4k\times \dfrac{3}{4}+1\times 1)^{2}}}{\vert 3k+1\vert }=\dfrac{6\sqrt{5}}{5}$,
当且仅当$k=\dfrac{3}{16}$时等号成立,
$\therefore \vert CD\vert$的最小值为$\dfrac{6\sqrt{5}}{5}$.
点评:本题考查直线与椭圆的综合运用,涉及了两点间的距离公式,利用二次函数的性质求最值,弦长公式等基础知识点,考查逻辑推理能力,运算求解能力,属于难题.
2022年高考数学浙江20<-->2022年高考数学浙江22
全网搜索"2022年高考数学浙江21"相关
|

