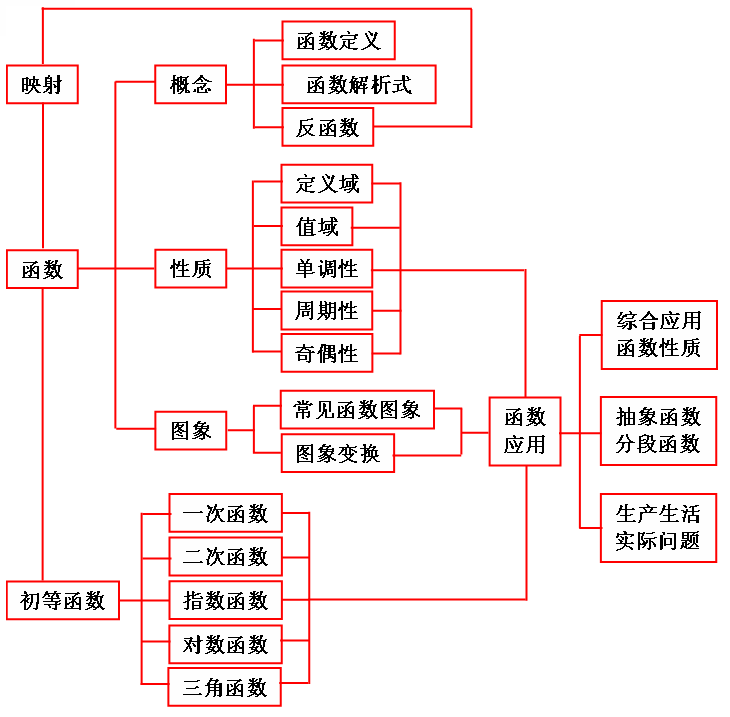
一、高考大纲
考试内容:
映射。函数。函数的单调性。奇偶性。
反函数。互为反函数的函数图像间的关系。
指数概念的扩充。有理指数幂的运算性质。指数函数。
对数。对数的运算性质。对数函数。
函数的应用。
考试要求:
(1)了解映射的概念,理解函数的概念。
(2)了解函数单调性、奇偶性的概念,掌握判断一些简单函数的单调性、奇偶性的方法。
(3)了解反函数的概念及互为反函数的函数图像间的关系,会求一些简单函数的反函数。
(4)理解分数指数幂的概念,掌握有理指数幂的运算性质,掌握指数函数的概念、图像和性质。
(5)理解对数的概念,掌握对数的运算性质。掌握对数函数的概念、图像和性质。
(6)能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题。
二、高考要览
| 考试内容 |
能力层次 |
高考要求 |
考题年份分值 |
| 映射与函数 |
理解 |
有关概念 |
|
2004 |
2005 |
2006 |
2007 |
2008 |
| 全国I.5 |
|
广东10.5 |
|
|
| 浙江.5 |
浙江.5 |
浙江10.5 |
|
|
| |
|
陕西12.5 |
|
|
| |
|
四川16.4 |
|
|
| 重庆.5 |
|
|
|
|
| 福建.4 |
|
|
|
|
| 北京.9 |
|
|
|
|
| |
江苏.4 |
|
|
|
| |
山东.5 |
|
|
|
| 湖南.5 |
|
|
|
|
| 湖北.5 |
|
|
|
|
|
函数的定义域
•解析式•值
域 |
掌握 |
有关概念 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| |
广东.4 |
广东1.5 |
|
|
| 重庆.5 |
|
重庆21.12 |
|
|
| |
|
辽宁13.4 |
|
|
| 湖南.5 |
湖南.5 |
湖南1.5 |
|
|
| |
|
湖北4.5 |
|
|
| 北京春.4 |
|
|
|
|
| 全国Ⅲ.5 |
|
|
|
|
| |
江苏.4 |
|
|
|
|
| 函数的单调性 |
掌握 |
判断一些简单函数单调性的方法 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| |
北京.5 |
北京5.5 |
|
|
| |
山东.5 |
山东18.12 |
|
|
| |
辽宁.5 |
|
|
|
| 上海.4 |
|
|
|
|
| |
重庆.5 |
|
|
|
| |
|
福建21.12 |
|
|
| |
|
广东3.5 |
|
|
|
| 函数的奇偶性 |
掌握 |
能利用函数的奇偶性与图象的对称性的关系描述函数图象 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| 全国. 5 |
|
全国8.5 |
|
|
| |
|
全国I16.4 |
|
|
| |
|
湖南14.4 |
|
|
| 福建.5 |
福建.5 |
|
|
|
| |
江西.4 |
江西1.5 |
|
|
| |
|
山东6.5 |
|
|
| |
|
辽宁2.5 |
|
|
| 上海.4 |
|
|
|
|
| |
广东.12 |
|
|
|
| |
天津.4 |
|
|
|
|
| 反函数 |
理解 |
反函数的概念及互为反函数图象间的关系 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| 全国.5 |
全国Ⅱ.5 |
|
|
|
| 湖南.5 |
湖南.4 |
|
|
|
| |
上海.4 |
上海3.4 |
|
|
| |
天津.5 |
|
|
|
| |
辽宁.5 |
|
|
|
| 江苏.5 |
江苏.5 |
|
|
|
| |
|
陕西4.5 |
|
|
| |
浙江.4 |
|
|
|
| |
|
安徽5.5 |
|
|
| |
|
福建8.5 |
|
|
|
| 掌握 |
会求一些简单函数的反函数 |
指数函数与
对数函数 |
掌握 |
指数函数与对数函数的概念图象和性质 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| 全国.5 |
全国I.4 |
全国Ⅱ6.5
全国Ⅱ20.12 |
|
|
| 北京春.4 |
北京春.4 |
|
|
|
| 广东.4 |
|
|
|
|
| 广西.5 |
|
|
|
|
| 辽宁.5 |
|
|
|
|
| 湖南.5 |
|
|
|
|
| 浙江.5 |
|
浙江3.5 |
|
|
| 福建.5 |
|
|
|
|
| 湖北.5 |
|
湖北21.14 |
|
|
| 天津.5 |
|
|
|
|
| 江苏.5 |
江苏.4 |
|
|
|
| |
上海.5
上海.4 |
|
|
|
| |
江西.5 |
|
|
|
| |
|
重庆15.4 重庆20.13 |
|
|
|
| 函数的图象 |
理解 |
有关概念 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| |
全国I.5
全国I.5 |
全国I2.5 |
|
|
| |
全国Ⅲ.5 |
|
|
|
| 福建.5 |
福建.4
福建.5 |
|
|
|
| 上海.4 |
|
|
|
|
| |
山东.5 |
山东2.5 |
|
|
| |
辽宁.5 |
|
|
|
| |
天津.5 |
|
|
|
| |
湖北.5 |
|
|
|
| |
广东.5 |
广东7.5 |
|
|
| 湖南.4 |
|
|
|
|
| |
|
重庆9.5 |
|
|
| |
|
江西12.5 |
|
|
|
| 利用函数知识解应用题 |
掌握 |
应用函数知识解决实际
难度问题 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| |
|
福建19.12 |
|
|
| 上海春.12 |
|
|
|
|
| 北京春.12 |
北京春.12 |
|
|
|
| |
|
江苏18.14 |
|
|
| |
|
湖南20.12 |
|
|
|
| 函数的综合问题 |
掌握 |
综合运用函数知识解决数学问题 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| |
|
全国II12.5 |
|
|
| 北京.12 |
|
|
|
|
| 上海.12 |
上海.5 |
|
|
|
| |
|
浙江12.5 |
|
|
| |
|
湖北10.5 |
|
|
| |
|
天津10.5 |
|
|
| |
|
辽宁7.5 |
|
|
| |
|
安徽15.4 |
|
|
| |
|
江西14.4 |
|
|
| |
|
广东20.16 |
|
|
| |
|
江苏20.14 |
|
|
|
三、命题趋势
从上表可以看出,近几年本章考查呈现以下特点:
1、题型和题量:三种题型(选择、填空、解答)都有,至少有4道题,一般3道客观题,2道解答题,分值30分以上,解答题中的一道往往与导数等综合.
2、知识点考查:
(1)映射与函数:以考查概念与运算为主,部分涉及新定义运算;
(2)定义域、值域、解析式是考查的重点,而且较稳定,有时结合其他知识点(以本部分内容为背景),分段函数较多、花样翻新;
(3)函数单调性在历年考试中久考不衰,且比例有上升趋势,和导数联系较多;
(4)函数的奇偶性主要和单调性、不等式、最值、三角函数等综合,与周期、对称性、方程等抽象函数问题联系多;
(5)反函数出现在填空、选择中,考反函数概念运算可能性大,若出现在解答题中,则必定与单调性、奇偶性、不等式、导数等知识综合,难度较大;
(6)二次函数问题是每年的必考题,一方面直接考查二次函数,另一方面是利用二次函数的性质解题,三个“二次”问题(即二次函数、二次方程、二次不等式)是函数考试题中永恒的主题;
(7)指数函数与对数函数以基本概念、性质为主设计试题,考查集中于指数、对数的定义域、值域、单调性和运算,选择、填空题属中等难度,若解答题涉及到指、对数函数,往往难度会上升;
(8)函数的图象每年必考,体现“形是数的直观反映,数是形的抽象概括”,是数学思想方法中“数形结合”思想的最直接的表现形式;尤其是函数`y=x+a/n(a>0)`的图象和性质,从1997年全国高考到2006年的试题,从未间断过;
(9)函数应用题与综合应用题是最能体现考生函数水平的试题:一次、二次函数、`y=x+a/n(a>0)`型、指数、对数型与现实生活中的SARS、禽流感等结合,必能产生新情景试题,是考查考生建模、应试能力的重点题型;而数列、不等式、向量、导数等众多知识点的交汇已成为函数综合应用中的典型问题.
3、难度与创新:函数作为贯穿整个高中学段的轴线,使其在高考中占据了举足轻重的地位,难度基本稳定在中等或稍偏上,但其特殊的地位,使函数的考查创新题型不断涌现,诸如分段函数、抽象函数、周期函数、凹凸性与定比分点结合、与导数结合、新定义题型等不一而足.
4、应用题:有诸多省市2006年试题涉及应用题,应用题仍为备考中应高度重视的重点对象.
四、复习建议
函数不仅是高中数学的核心内容,还是学习高等数学的基础,所以函数知识在高考中占有极其重要的地位.试题不但形式多样,而且突出考查学生联系与转化、分类与讨论、数与形结合等重要的数学思想、能力,知识覆盖面广、综合性强、思维力度大、能力要求高,是高考中考数学思想、数学方法、考能力、考素质的主要知识.所以,复习中力争做到:
1、定位准确
(1)深刻理解函数的有关概念,掌握对应法则、图象等有关性质.
(2)理解掌握函数的单调性和奇偶性的概念,并掌握基本的判定、证明方法,能利用导数等工具研究函数的单调性(周期性)等性质.
(3)掌握反函数的概念,明确反函数的意义,求反函数的步骤与方法,明确求函数定义域(值域)、解析式的基本方法.
(4)掌握指数函数和对数函数的性质、图象、运算,注意初等函数(包括二次函数)的应用,注意数学模型的建立方法.
2、明确命题趋势
函数的基础地位决定了函数试题较多,高、中、低档题目全有,题型齐全,重难点突出,创新容易,与其他知识块联系较多,像函数的凹凸性、分段函数、周期函数、新定义新情景题层出不穷.复习中应注意捕捉此类信息,注重新题训练,防止新颖考题呈现于面前而无从下手的情形出现.
3、注重基础,抓住基本函数、结合数学思想,联系实际应用
(1)熟练掌握二次函数、反比例函数、指数对数函数以及形如`y=x+a/n(a>0)`的函数的性质,重点从定义域、值域、单调性、奇偶性、反函数等方面提炼归纳,特别是以上述几种函数为模型的抽象函数.
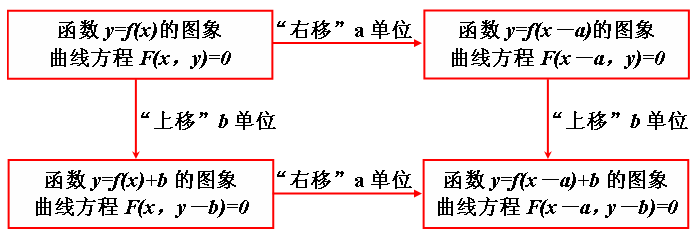
(2)注意与图象、图表相关的问题,能从图表中读取各种信息,注意利用平移、伸缩、对称变换,培养数形结合的能力.反函数问题是此类问题的典型,新定义、新情景问题也大多以图表形式给出,要以基本函数为基础强化南式到图和由图到式的转化训练.
(3)指数、对数函数试题多数与其他函数组合为复合函数,是重点题型之一.多以方程或二次函数为背景,综合考查函数、方程和不等式的知识,注重代数推理能力,一般要转化为二次函数或利用导数求解,应掌握常见题的解题方法和思路,构建思维模式.
五、思想与方法综览
1、数形结合思想
数形结合的解题方法,就是把数学问题中的数量关系和空间形式结合起来考虑的思维方法,其实质就是将抽象的数学语言与直观的图形结合起来,抽象思维和形象思维结合起来,使抽象问题具体化,复杂问题简单化,通过“数”和“形”的联系和转化,化难为易,从而使问题得以解决.
[案例]若函数`y=(1/2)^(|1-x|)+m`的图象与x轴有公共点,则m的取值范围是(
)
A.m≤-1 B.-1≤m<0 C.m≥1 D.0<m≤1
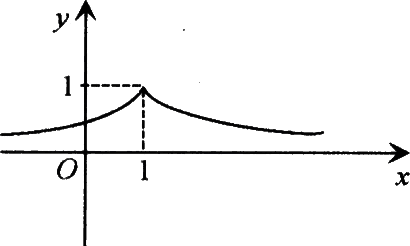
解:首先作出`y=(1/2)^(|1-x|)`的图象(如图),
欲使`y=(1/2)^(|1-x|)+m`的图象与轴有交点,则-1≤m<0.
[案例]已知关于x的方程`x^2+(1/2-2m)x+m^2-1=0`(m是与x无关的实数)的两个实根在区间[O,2]内,求m的取值范围.
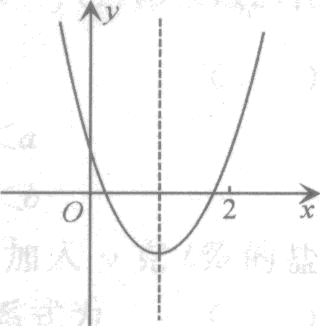
解:设函数`f(z)=x^2+(1/2-2m)x+m^2-1`,由图知
,方程的两根都在区间[0,2]内的充要条件为
`{((1/2-2m)^2-4(m^2-1)>=0),(0<(2m-1/2)/2<2),(f(0)=m^2-1>=0),(f(2)=4+2(1/2-2m)+m^2-1>=0):}`
即`{(m<=17/8),(1/4<m<9/4),(m<=-1或m>=1),((m-2)^2>=0):}`
故m的取值范围为`[1,17/8]`.
2、分类讨论思想
解答数学题时有时无法用同一种形式去解决,而需要选定一个标准,根据这个标准将问题划分成几个能用不同形式去解决的问题将这些小问题一一加以解决,从而使问题得到解决,这就是分类讨论思想.
[案例]已知函数`f(x)=a^x-2sqrt(4-a^x)-1`(a>O,a≠1).
(1)求函数f(x)的定义域、值域;
(2)是否存在实数a,使得函数f(x)满足:对于区间`(2,+oo)`上的一切x,都有f(x)≥O.
分析:就a进行分类讨论,确定定义域,通过换元法考查函数的值域.
解:(1)由`4-a^x`≥O,得`a^x`≤4.
当n>1时,x≤`text(log)_a4`;当O<a<1时,x≥`text(log)_a4`.
即当n>1时,f(x)的定义域为`(-oo,text(log)_a4]`;
当O<a<1时,f(x)的定义域为`[text(log)_a4,+oo)`.
令`t=sqrt(4-a^x)`,则0≤t<2,且`a^x=4-t^2`,
`:.`原函数则变为`g(t)=4-t^2-2t-1=-(t+1)^2+4`,
当t≥O时,g(f)是t的单调减函数,
`:.`g(2)<g(t)≤g(O),即-5<g(t)≤3,
`:.`g(t)的值域为(-5,3],即函数f(x)的值域是(-5,3].
(2)若存在实数n使得对于区间`(2,+oo)`上使函数f(x)有意义的一切x,都有f(x)≥0,则区间`(2,+oo)`是定义域的子集.
由(1)知,a>1不满足条件;
若O<a<l,则`text(log)_a`4<2,且f(x)是x的减函数.
当x>2时,`a^x<a^2`.
由于`0<a^2<1,:.t=sqrt(4-a^x)>sqrt(3)`,
`.:`t>-1时,g(t)为减函数,且当t=1时g(t)=O,
`:.t>sqrt(3)时,g(t)<0,
即f(x)<O,`:.`f(x)≥O不成立.
综上,满足条件的n的取值范围是`O/`.
点评:注意用整体的思想处理问题.在解题时,为将指数式或对数式转化为熟知的代数式,常采用换元的方法.分类讨论是学习本考点知识必须牢记的思想方法,分类的标准往往是底数的取值.
3、等价转化思想
[案例]若不等式`x^2+px>4x+p-3`,对于一切0≤p≤4均成立,则实数x的取值范围是_____.
解:原不等式转化为关于p的一次不等式
p(x-1)+`x^2`-4x+3>0.
由题意设f(p)=p(x-1)+`x^2`-4x+3,在p∈[O,4]时,f(p)>0成立,
`:.{(f(0)>0),(f(4)>0):}
:.{(x^2-4x+3>0),(x^2-1>0):}`
`:.`x>3或x<-1.
答案:{x|x>3或x<-1}.
4、函数与方程思想
函数思想是指用联系变化的观点分析问题,通过函数的形式把问题中的数量关系表示出来,运用函数的概念、图
象、性质等对问题加以研究,使问题获得解决.
方程的思想是指将问题转化为对方程(组)的认识,通过解方程或对方程的讨论使问题得以解决.
函数与方程二者密不可分,如函数解析式y=f(x)也可看做方程,函数有意义则方程有解,方程有解,则函数有意义等.函数与方程思想体现了动与静、变量与常量的辩证统一,是重要的数学思想方法之一.
[案例](2006·全国Ⅱ)已知a∈R,二次函数`f(x)=ax^2-2x-2a`.若f(x)>O的解集为A,又知集合B={x|1<
x<3},`A nn B≠O/`,求实数a的取值范围.
解:方法一:(1)若a=O,f(x)=-2x,f(x)>0 `hArr` x<0,此时`A nn
B=O/`不合题意.
若a≠0,由`△=4+8a^2>0`知,f(x)有两个不等实根:`x_1=1/a-sqrt(2+1/a),x_2=1/a+sqrt(2+1/a)`
由`x_1x_2=-2<0`知,`x_1<O,x_2>O`.
①当a>O时,`A={x|x<x_1} uu {x|x>x_2}`,
`A nn B=O/ hArr x_2<3 hArr 1/a+sqrt(2+1/a)<3 hArr
a>6/7`.
②当a<O时,`A={x|x_1<x<x_2}`,
`A nn B=O/ hArr x_1>0 hArr 1/a+sqrt(2+1/a)>1 hArr a<-2`
综上,使`A nn B≠O/`成立的`a`的取值范围为`(-oo,-2) uu (6/7,+oo)`.
方法二:(1)若a=O,则f(x)=-2x.
由f(x)>0,解得x<0.
此时`A nnB=O/`,不合题意.
(2)若a≠0,由`△=4+8a^2>0`知,f(x)有两个不等实根`x_1`,`x_2`,设`x_1<x_2`.
又由韦达定理知`x_lx_2=-2<0`,故`x_1<0<x_2`.
①当a>0时,`A nn B≠O/ hArr f(3)>0 hArr 7a>6 hArr a>6/7`.
②当a<O时,`A nn B≠O/ hArr f(1)>0 hArr -a-2>0 hArr a<-2`.
综上,使`A nn B`成立的`a`的取值范围为`(-oo,-2) uu (6/7,+oo)`.
|