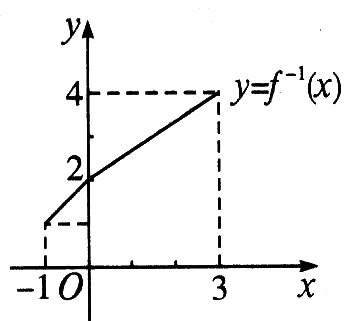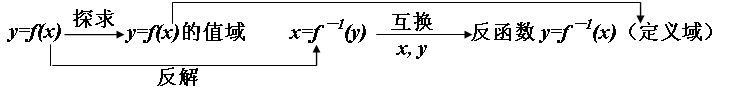§2.6 反函数

第二章函数
§2.6 反函数

复习目标

知识梳理

应用举例

实践体验

拓展探究

基础训练

提高训练

学习感悟

一、复习目标
了解反函数的概念及互为反函数的图象间的关系，会求一些简单函数的反函数.

二、重点难点
重点:反函数的概念及互为反函数的图象间的关系, 掌握求反函数的步骤.

难点:会求简单函数的反函数.

    三、特别提示
    1、单调函数存在反函数，但是存在反函数不一定单调，如函数 $f (x) = \frac{1}{x}$ ．
    2、求反函数一要注意在开方时“±”的确定，由原函数的定义域决定；二要注意注明反函数的定义域，特别是当使反函数的解析式有意义的自变量的取值集合与反函数的定义域不相等时更要注明其定义域．
    3、反函数的有关问题可以通过原函数来研究，反之亦然．

    知识梳理
    1、反函数
    设y=f(x)表示y是变量x的函数，其定义域为A，值域为C，从式子y=f(x)中解得x=g(y)，如果x=g(y)表示x是自变

量y的函数，那么把x=g(y)叫做函数y=f(x)的反函数，记作

y = f^{- 1} (x)

．

习惯上用x表示自变量，y表示函数，函数y=f(x)的反函数记作y=

f^{- 1} (x)

．函数f(x)的定义域是它的反函数的值域，其值域是它的反函数的定义域．

2、互为反函数的函数图象间的关系

函数y=f(x)的图象和它的反函数

y = f^{- 1} (x)

的图象关于直线y=x对称．

3．求函数y=f(x)的反函数的一般步骤是

(1)确定原函数的值域，也就是反函数的定义域；

(2)由y=f(x)的解析式求出x=g(x)；

(3)将x、y对换，得反函数的一般表达式

y = f^{- 1} (x)

．

    应用举例
    一、应用特点
    1、如何求反函数；
    2、原函数与反函数的图象关系的变式运用；
    3、求分段函数的反函数.

二、案例示范
(回味相关知识与方法，寻找解题办法，若有困难，可以参考“提示”，还有困难，可以参考“解答”或倾听老师的分析示范)

    1、函数 $y = {\begin{cases} 2 x ， x \geq 0 ， \\ - x^{2} ， x ＜ 0 ， \end{cases}$ 的反函数是(   )
    A. $y = {\begin{cases} \frac{x}{2} ， x ＞ = 0 \\ \sqrt{- x} ， x ＜ 0 \end{cases}$      B. $y = {\begin{cases} 2 x ， x ＞ = 0 \\ \sqrt{- x} ， x ＜ 0 \end{cases}$
    C. $y = {\begin{cases} \frac{x}{2} ， x ＞ = 0 \\ - \sqrt{- x} ， x ＜ 0 \end{cases}$     D. $y = {\begin{cases} 2 x ， x ＞ = 0 \\ - \sqrt{- x} ， x ＜ 0 \end{cases}$

提示	示范
先将x用y来表示，即将x反解出来，再将变量x、y互换，最后求出原函数的值域，即反函数的定义域.
解:有关分段函数的反函数的求法，可用特殊点排除法，原函数上有(1，2)和(-1，-1)两点，反函数上应有(2，1)和(-1，-1)，检验知C正确．答案：C 评注:求反函数的定义域时，一定要通过求原函数的值域来实现，否则容易出错．

2、已知

f (x) = \frac{1 - 2 x}{1 + x}

，函数g(x)的图象与函数

y = f^{- 1} (x + 1)

的图象关于直线y=x对称，则g(5)=___．

提示	示范
找出题中的原函数、反函数以及它们之间的关系，再通过原函数、反函数的变量取值的对应关系求出g(5)的值.
解: $y = f^{- 1} (x + 1) \Rightarrow f (y) = f [f^{- 1} (x + 1)] = x + 1 ， x = f (y) - 1$ ， ∴y= $f^{- 1} (x + 1)$ 的反函数y=f(x)-1，即g(x)=f(x)-l．∴g(5)=f(5)-1= $- \frac{5}{2}$ ．答案： $- \frac{5}{2}$ 评注:求函数的反函数就是要把x从函数解析式中求出来，这就要看施加在x上的运算有几层，各是什么，然后从外向里用每层运算的逆运算加在等号两边，x就可以逐步“解放”出来，这就是解法一的思想．平移法、图象法也可求反函数，显得更形象、直观、易解．

3、求函数

f (x) = {\begin{cases} x^{2} + 1 ， x \leq - 1 ， \\ - x + 1 ， x ＞ - 1 \end{cases}

的反函数．

提示	示范
按照求反函数的步骤分段去求.
解:当x≤-1时， $y = f (x) = x^{2} + 1$ ≥2．又由 $y = x^{2} + 1$ ，得x=-sqrt(y-1)． ∴ $f^{- 1} (x) = - \sqrt{x - 1}$ ，x≥2．当x＞-1时，y=f(x)=-x+1＜2．由y=-x+1，得x=1-y． ∴ $f^{- 1} (x)$ =1-x，x＜2．故 $f^{- 1} (x) = {\begin{cases} 1 - x ， x ＜ 2 ， \\ - \sqrt{x - 1} ， x \geq 2 . \end{cases}$ 评注:反函数的定义域是原函数的值域，因此要分段去求原函数值域．另外，分段函数的反函数也要写成分段形式

    实践体验
    (在实践中提高能力，在体验中反思感悟，力求独立，力求提高)
    1、函数f(x)=ln(x-1)(x＞1)的反函数是(   )

A．

f^{- 1} (x) = e^{x} + 1

(x∈R)

B．

f^{- 1} (x) = 10^{x} + 1

(x∈R)

C．

f^{- 1} (x) = 10^{x} + 1

(x＞1)

D．

f^{- 1} (x) = e^{x} + 1

(x＞1)

提示	示范
注意反函数的定义域.
解:(1)设y=ln(x-1)(x＞1)， ∴ $x - 1 = e^{y} ， x = e^{y} + 1$ (y∈R)． ∴ $f^{- 1} (x) = e^{x} + 1$ (x∈R)．故选A．答案：A. 评注:掌握求反函数的三个步骤，准确地求出反函数．

2、函数f(x)有反函数

f^{- 1} (x)

，已知f(x)图象经过点(O，-1)，则

f^{- 1} (x + 4)

的反函数图象必过点( )

提示	示范
互为反函数的点的坐标特点是横纵坐标互换,在平移可得所过的定点.
解:由于f(x)的图象经过点(0，-1)，则 $f^{- 1} (x)$ 的图象经过点(-1，0)，而 $f^{- 1} (x + 4)$ 是将 $f^{- 1} (x)$ 的图象向左平移4个单位而得到，故过点(-5，0)．评注:由于互为反函数的函数图象关于直线y=x对称，因而点(O，-1)在y=(x)的图象上，那么点(-1，O)必在 $y = f^{- 1} (x)$ 的图象上．

拓展探究
已设a＞1，函数f(x)=

a^{x + 1}

-2．

(1)求f(x)的反函数

f^{- 1} (x)

；

(2)若

f^{- 1} (x)

在[O，1]上的最大值与最小值互为相反数，求a的值；

(3)若

f^{- 1} (x)

的图象不经过第二象限，求a的取值范围．

提示	示范
先求反函数,进而分析其单调性与过定点的特征, 有利问题的解决.
解:(1)∵ $a^{x + 1}$ ＞0 ∴f(x)的值域是{y\|y＞-2}. 设 $y = a^{x + 1} - 2$ ,解得 $x = {log}_{a} (y + 2) - 1$ 所以f(x)的反函数 $f^{- 1} (x) = {log}_{a} (x + 2) - 1 (x ＞ 2)$ (2)当a＞1时,函数 $f^{- 1} (x) = {log}_{a} (x + 2) - 1$ 为(-2,+∞)上的增函数，所以 $f^{- 1} (0) + f^{- 1} (1) = 0$ , 即 $({log}_{a} 2 - 1) + ({log}_{a} 3 - 1) = 0$ 解得 $a = \sqrt{6}$ . (3)当a＞1时,函数 $f^{- 1} (x)$ 为(-2,+∞)上的增函数,且经过定点(-1,-1). 所以 $f^{- 1} (x)$ 的图象不经过第二象限的充要条件是 $f^{- 1} (x)$ 的图象与x轴的交点位于x轴的非负半轴上. 令 ${log}_{a} (x + 2) - 1 = 0$ ,解得x=a-2, 由a-2≥0,解得a≥2. 评注:求反函数要注意求其定义域,即求原函数的值域.注意函数单调性与函数最值的关系,注意函数过定点的重要作用.

基础训练

1、函数

y = {log}_{2} \frac{x}{x - 1}

(x＞1)的反函数是( )
A.

y = \frac{2^{x}}{2^{x} - 1}

(x＞0) B.

y = \frac{2^{x}}{2^{x} - 1}

(x＜0)
C.

y = \frac{2^{x} - 1}{2^{x}}

(x＞0) D.

y = \frac{2^{x} - 1}{2^{x}}

(x＜0)
2、若函数f(x)的反函数为

f^{- 1} (x) = 2^{x + 1}

，则f(1)的值为(   )
    A．4   B．-4   C．1   D．-1
    3、设函数

f (x) = {log}_{a} (x + b) (a ＞ 0 ， a \neq 1)

的图象过点 (2，1)，其反函数的图象过点(2，8)，则a+b等于(   )
    A．6   B．5   C．4   D．3
    4、函数y=

ln (x + \sqrt{x^{2} + 1})

(x∈R)的反函数为( )
A．

y = \frac{1}{2} (e^{x} - e^{- x})

，x∈R
B．

y = \frac{1}{2} (e^{x} - e^{- x})

，x∈(0，+∞)
C．

y = \frac{1}{2} (e^{x} + e^{- x})

，x∈R
D．

y = \frac{1}{2} (e^{x} + e^{- x})

，x∈(0，+∞)
5、函数y=f(x)的反函数y=f^-1(x)的图象与y轴交于点P(0，2)(如图所示)，则方程f(x)=O，在[1，4]上的根是x=______．

6、已知两个函数的图象关于直线y=x对称，如果其中一个函数是y=-sqrt(x-1)(x≥1)，那么另一个函数是______．
7、设函数

y = f (x)

(x∈A)是增函数，证明它的反函数

y = f^{- 1} (x)

(x∈B)是增函数．
8、已知函数y=2^(1-x)+3(x∈R)，求它的反函数的解析表达式．

参考答案

1、函数

y = {log}_{2} \frac{x}{x - 1}

(x＞1)的反函数是( A )
A.

y = \frac{2^{x}}{2^{x} - 1}

(x＞0) B.

y = \frac{2^{x}}{2^{x} - 1}

(x＜0)
C.

y = \frac{2^{x} - 1}{2^{x}}

(x＞0) D.

y = \frac{2^{x} - 1}{2^{x}}

(x＜0)
2、若函数f(x)的反函数为

f^{- 1} (x) = 2^{x + 1}

，则f(1)的值为( D )
A．4 B．-4 C．1 D．-1
3、设函数

f (x) = {log}_{a} (x + b) (a ＞ 0 ， a \neq 1)

的图象过点 (2，1)，其反函数的图象过点(2，8)，则a+b等于( C )
A．6 B．5 C．4 D．3
4、函数y=

ln (x + \sqrt{x^{2} + 1})

(x∈R)的反函数为( A )
A．

y = \frac{1}{2} (e^{x} - e^{- x})

，x∈R
B．

y = \frac{1}{2} (e^{x} - e^{- x})

，x∈(0，+∞)
C．

y = \frac{1}{2} (e^{x} + e^{- x})

，x∈R
D．

y = \frac{1}{2} (e^{x} + e^{- x})

，x∈(0，+∞)
5、函数y=f(x)的反函数y=f^-1(x)的图象与y轴交于点P(0，2)(如图所示)，则方程f(x)=O，在[1，4]上的根是x=______．

    答案:2
    6、已知两个函数的图象关于直线y=x对称，如果其中一个函数是y=-sqrt(x-1)(x≥1)，那么另一个函数是______．
    答案:

y = x^{2} + 1

(x≤0)
7、设函数

y = f (x)

(x∈A)是增函数，证明它的反函数

y = f^{- 1} (x)

(x∈B)是增函数．
    答案:(略)
    8、已知函数y=2^(1-x)+3(x∈R)，求它的反函数的解析表达式．
    答案:

y = {log}_{2} \frac{2}{x - 3} (x ＞ 3)

提高训练

1、已知

f (x) = \frac{a - x}{x - (a + 1)} ， 且 f^{- 1} (x - 1)

的图象的对称中心是(0，3)，则a的值为( )
A．

\sqrt{2}

B．2 C．

\sqrt{3}

D．3
2、要使

y = x^{2} + 2 x

(x≤a)有反函数，则a的最大值为______.
3、求与方程

y = e^{2 x} - 2 e^{x} + 1

(x≥0)的曲线关于直线y=x对称的曲线的方程．
4、设函数

f (x) = {log}_{2} \frac{2 x - 1}{2 x + 1} (x ＜ - \frac{1}{2} 或 x ＞ \frac{1}{2})

的反函数为

f^{- 1} (x)

．
(1)证明

f^{- 1} (x)

是奇函数；
(2)求

f^{- 1} (x)

的单调区间．

参考答案

1、已知

f (x) = \frac{a - x}{x - (a + 1)} ， 且 f^{- 1} (x - 1)

的图象的对称中心是(0，3)，则a的值为( B )
A．

\sqrt{2}

B．2 C．

\sqrt{3}

D．3
2、要使

y = x^{2} + 2 x

(x≤a)有反函数，则a的最大值为______.
答案:-1
3、求与方程

y = e^{2 x} - 2 e^{x} + 1

(x≥0)的曲线关于直线y=x对称的曲线的方程．
答案:

f^{- 1} (x) = ln (1 + \sqrt{x})

4、设函数

f (x) = {log}_{2} \frac{2 x - 1}{2 x + 1} (x ＜ - \frac{1}{2} 或 x ＞ \frac{1}{2})

的反函数为

f^{- 1} (x)

．
(1)证明

f^{- 1} (x)

是奇函数；
(2)求

f^{- 1} (x)

的单调区间．
答案:(1)(略)；(2)

f^{- 1} (x)

的单调增区间为(0,+∞)和(-∞,0)

    学习感悟
    1、要深入理解函数 $y = f (x)$ 与其反函数 $y = f^{- 1} (x)$ 的概念：

    $y = f (x)$ 和 $x = f^{- 1} (y)$ 互为反函数，但在同一坐标系下的图象相同.
    2、求函数 $y = f (x)$ 的反函数 $x = f^{- 1} (y)$ 的一般步骤如下：

    3、恰当利用函数与其反函数的关系，可以将“反函数”有关问题转化为“原函数”问题，往往可以巧妙地解决一类问题．

本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。