|
一、复习目标 能够运用函数的性质、指数函数、对数函数的性质解决某些简单的实际问题,培养应用函数知识解决实际问题的能力. 二、重点难点 难点:综合运用函数思想及方法分析与解决问题的能力. 三、特别提示 |
| 知识梳理 1、函数是指在某一变化过程中两个变量的对应关系. 2、列举几个常用的求最值的方法. 3、函数单调性的判定方法有定义法、求导法等. 4、解答函数应用题的一般步骤为 (1)审题:理解题意,把握数学本质; (2)建模:分析题中的数量关系,建立相应数学模型,将应用问题转化为数学问题; (3)解模:用数学知识与方法解决转化了的数学问题; (4)回验:回到应用问题,检验结果的实际意义,给出答案. 此四步用框图可表示为 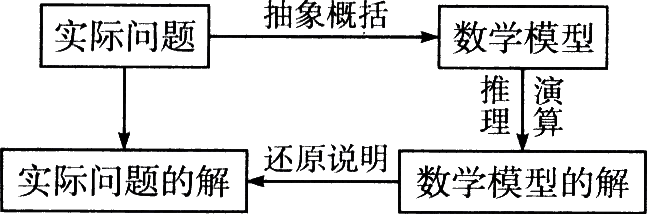 |
|
应用举例 二、案例示范
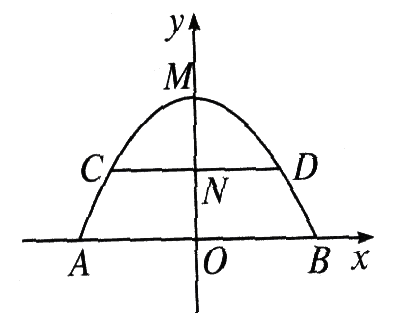
1、下图是抛物线形拱桥,已知水位在AB位置时,水面宽`4sqrt(6)`m,水位上升3m就达到警戒线CD,这时水面宽`4sqrt(3)`m.若洪水到来时,水位以每小时0.25 m的速度上升,求水过警戒线后几小时淹到拱桥顶?
2、用长为m的铁丝弯成下部为矩形,上部为半圆形的框架(如图),若矩形底边长为2x,求此框架的面积y与x的函数式,并写出它的定义域. 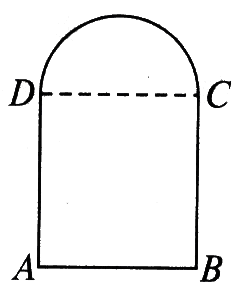
3、市场营销人员对过去几年某商品的价格及销售数量的关系作数据分析发现有如下规律:该商品的价格每上涨x%(x>0),销售数量就减少kx%(其中k为正常数).目前,该商品定价为a元,统计其销售数量为b个. (1)当k=`1/2`时,该商品的价格上涨多少,才能使销售的总金额达到最大? (2)在适当的涨价过程中,求使销售总金额不断增加时k的取值范围.
|
| 实践体验 (在实践中提高能力,在体验中反思感悟,力求独立,力求提高) 1、现代社会对破译密码的难度要求越来越高,有一种密码把英文的明文(真实文)按字母分解,其中英文的a.b,c,…,z,26个字母(不论大小写)依次对应1,2,3,…,26个自然数.见下面表格.
`y={((x+1)/2text(,)x in N text(,) 1<=x<=26 text(,)x不能被2整除),(x/2+13text(,)x in N text(,) 1<=x<=26 text(,)x能被2整除):}` 将明文转换为密文,如 `6 rarr 6/2+13=16`,即将f变成p,即f`rarr`p. `9 rarr (9+1)/2=5`,即将i变成e,即i`rarr`e. (1)按上述方法将明文good译成密文; (2)若按上述方法将某明文译成的密文是shxc,请你找出它的明文.
2、2005年10月12日,我国成功发射了“神舟”六号载人飞船,这标志着中国人民又迈出了具有历史意义的一步.已知火箭的起飞重量M是箭体(包括搭载的飞行器)的重量m和燃料重量x之和.在不考虑空气阻力的条件下,假设火箭的最大速度y关于x的函数关系式为y=k[ln(m+x)-ln(`sqrt(2)`m)]+4ln2(其中k≠0).当燃料重量为(`sqrt(e)`-1)m吨(e为自然对数的底数,e≈2.72)时,该火箭的最大速度为4 km/s. (1)求火箭的最大速度y(km/s)与燃料重量x吨之间的函数关系式y=f(x); (2)已知该火箭的起飞重量是544吨,则应装载多少吨燃料,才能使该火箭的最大飞行速度达到8km/s,顺利地把飞船发送到预定的轨道?
|
| 拓展探究 已知定义域为R的函数`f(x)=(-2^x+b)/(x^(x+1)+a)`是奇函数. (1)求a、b的值; (2)若对任意的t∈R,不等式`f(t^2-2t)+f(2t^2-k)<0`恒成立,求k的取值范围.
|
|
|
|
|
学习感悟 |