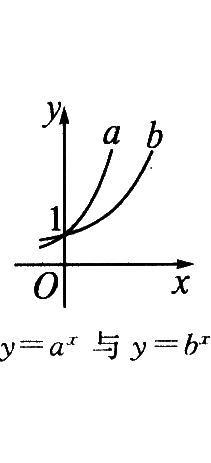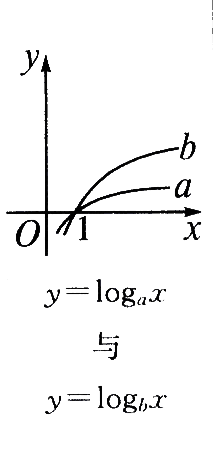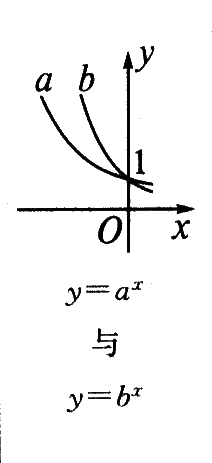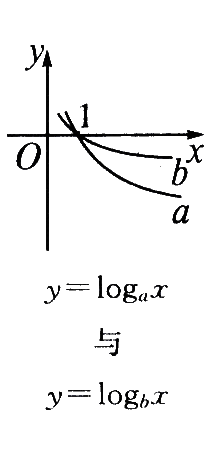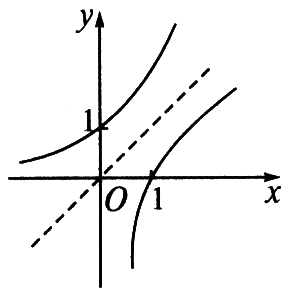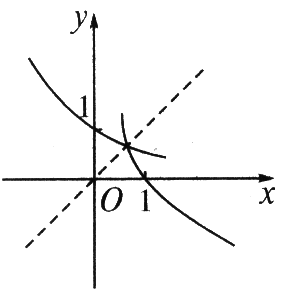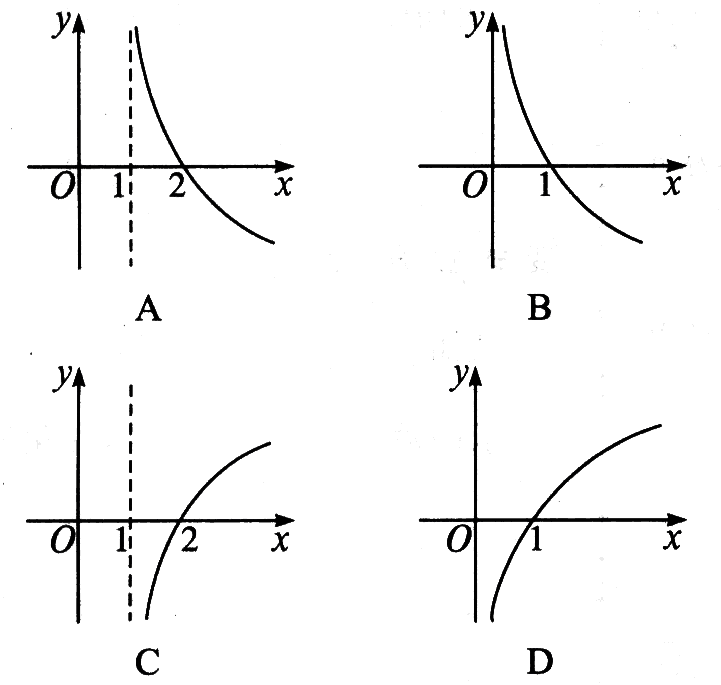二、重点难点
    重点:指﹑对数的运算性质, 指﹑对数函数的概念、图象和性质.

    难点:指﹑对数函数的概念、图象和性质的综合应用.

    三、特别提示
    1、式的运算、变形、求值、化简及证明在数学中占有重要地位，是研究方程、不等式和函数的基础，应引起重视；
    2、指数函数`y=a^x`与对数函数`y=log_ax(a＞0，且a≠1)`互为反函数，可从概念、图象、性质几方面理解它们的联系与区别；
    3、比较两个幂值的大小是一种常见的题型，也是一类容易做错的问题．解决这类问题，首先要分清是底数相同还是指数相同，如果底数相同，可利用指数函数的单调性；如果指数相同，可利用图象(如下表)．
    同一坐标系下的图象关系：

    当底大于1时，底越大图象越靠近坐标轴，当底小于1大于O时，底越小，图象越靠近坐标轴，如果底数、指数都不同，则要利用中间变量．
    4、指数函数、对数函数中绝大部分问题是指数函数、对数函数与其他函数的复合函数问题，讨论复合函数的单调性是解决这类问题的重要途径之一．

    知识梳理
    1、指数幂的概念
    (1)根式
    如果一个数的n次方等于a(n＞1，且n∈`N^**`)，那么这个数叫做a的n次方根．也就是，若`x^n=a`，则x叫做底数，
其中n＞1，且n∈`N^**`．式子`root(n)(a)`叫做根式，这里n叫做根指数，a叫做被开方数．
    (2)根式的性质
    ①当n为奇数时，正数的n次方根是一个正数，负数的n次方根是一个负数，这时，a的n次方根用符号`root(n)(a)`表示．

    ②当n为偶数时，正数的n次方根有两个，它们互为相反数，这时,正数的正的n次方根用符号`root(n)(a)`表示，负的n次方根用符号`-root(n)(a)`表示．正 负两个n次方根可以合写为`+-root(n)(a)(a＞0)`.

    ③`(root(n)(a))^n=a`．

    ④当n为奇数时，`root(n)(a^n)=a`；当n为偶数时，`root(n)(a^n)=|a|`.

    ⑤负数没有偶次方根．

    ⑥零的任何次方根都是零．
    (3)分数指数幂的意义
    ①`a^(m/n)=root(n)(a^m) (a＞0，m、n in N^**，且n＞1)`；
    ②`a^(-m/n)=1/(a^(m/n)) (a＞0，m、n in N^**，且n＞1)`．
    (4)有理数指数幂的运算性质
    ①`a^r*a^s=a^(r+s)`(a＞0，r∈Q，s∈Q)；
    ②`a^r-:a^s=a^(r-s)`(a＞0，r∈Q，s∈Q)；
    ③`(a^r)^s=a^(rs)`(a＞0，r∈Q，s∈Q)；
    ④`(ab)^r=a^rb^r`(a＞0，b＞0，r∈Q)．
    2、对数
    (1)对数的概念：如果`a(a＞0，n≠1)`的`b`次幂等于`N`，就是`a^b`=N，那么，数`b`叫做以`a`为底`N`的对数，记作`log_aN``=``b`，其中a叫做对数的底数，N叫做对数的真数．
    (2)常用对数：通常将`log_(10)N`的对数叫做常用对数，记作`lgN`.
    自然对数：通常将以无理数`e=2.718 28…`为底的对数叫做自然对数，记作`lnN`．
    (3)对数的性质
    ①零和负数没有对数；
    ②`log_a1=0 (a＞0，a≠1)；
    ③`log_aa=1 (a＞0，n≠1)；
    ④`a^(log_aN)=N (a＞0，n≠1，N＞0)`．
    3、对数的运算性质
    如果`a＞0`，`a≠1`，`M＞O`，`N＞0`，那么
    (1)`log_a(MN)=log_aM+log_aN`；
    (2)`log_aM/N=log_aM-log_aN`；
    (3)`log_aM^n=nlog_aM(n∈R)`．
    4、基本概念
    (1)对数函数的概念：
    函数`y=log_ax`叫做对数函数，其中a是一个大于零且不等于1的常量，函数的定义域是(0,+∞)；
    (2)指数函数的概念：函数`y=a^x`(其中`a＞0`且`a≠1`)叫做指数函数；
　　(3)指数函数与对数函数互为反函数．
    5、指数函数、对数函数的图象及性质

    应用举例
    一、应用特点
    1、两个幂的大小比较;对数的运算性质及换底公式的应用.
    2、指数函数的概念、图象和性质;对数函数的图象和性质的应用.
    3、指数函数与其他函数的综合问题;对数函数与其他知识的综合应用.

    二、案例示范
    (回味相关知识与方法，寻找解题办法，若有困难，可以参考“提示”，还有困难，可以参考“解答”或倾听老师的分析示范)

    1、(1)三个数`6^(0.7)、0.7^6、text(log)_(0.7)6`的大小顺序是(   )
    A.`0.7^6＜text(log)_(0.7)6＜6^(0.7)`     B.`0.7^6＜6^(0.7)＜text(log)_(0.7)6`
    C.`text(log)_(0.7)6＜6^(0.7)＜0.7^6`     D.`text(log)_(0.7)6＜0.7^6＜6^(0.7)`
    (2)已知x，y，z＞0且lgx+lgy+lgz=0，求`x^(1/(text(lg)y)+1/(text(lg)z))·y^(1/(text(lg)z)+1/(text(lg)x))·z^(1/(text(lg)x)+1/(text(lg)y)`的值

提示	示范
(1)尽管`text(log)_(0.7)6`不是幂的形式，但它是个负值．因此关键是比较两个正数`6^(0.7)`与`0.7^6`的大小，可用中间值“1”比较.     (2)由于所求式子的形式是三项积的形式，每一项又都有指数，指数中又有对数，因此想到用对数的运算法则，如果能对所求式子取对数，那可能会好解决些．故想到用参数法，设所求式子的值为t．
解:(1)∵`text(log)_(0.7)6＜0,0.7^6＞0,6^(0.7)＞0`,∴`text(log)_(0.7)6`最小．     又0＜`0.7^6`＜1，`6^(0.7)`＞1，∴`0.7^6＜1＜6^(0.7)`．因此选D．     答案：D     (2)令`x^(1/(text(lg)y)+1/(text(lg)z))·y^(1/(text(lg)z)+1/(text(lg)x))·z^(1/(text(lg)x)+1/(text(lg)y)`=t，则     `text(lg)t=(1/(text(lg)y)+1/(text(lg)z))·text(lg)x+(1/(text(lg)z)+1/(text(lg)x))·text(lg)y+(1/(text(lg)x)+1/(text(lg)y))·text(lg)z`     =`(text(lg)x)/(text(lg)y)+(text(lg)x)/(text(lg)z)+(text(lg)y)/(text(lg)z)+(text(lg)y)/(text(lg)x)+(text(lg)z)/(text(lg)x)+(text(lg)z)/(text(lg)y)`     =`(text(lg)x+text(lg)z)/(text(lg)y)+(text(lg)x+text(lg)y)/(text(lg)z)+(text(lg)y+text(lg)z)/(text(lg)x)`     =`(-text(lg)y)/(text(lg)y)+(-text(lg)z)/(text(lg)z)+(-text(lg)x)/(text(lg)x)`     =-3     ∴`t=10^-3=1/1000`即为所求．     评注:(1)利用指数函数的单调性比较大小，通常需要选一个中间量．中间量的选取比较灵活，其基本原则是：中间量与两个指数的底数或指数相同．

    2、(1)在`P(1，1)`、`Q(1，2)`、`M(2，3)`和`N(1/2，1/4)`四点中，函数`y=a^x`的图象与其反函数的图象的公共点只可能是点(   )
    A．P     B．Q     C．M     D．N
    (2)根据下列不等式确定a的取值范围：
    ①`text(log)_a2/3`＜1；②`text(log)_a(1-2a)`＜1；③`text(log)_a(1-2a)`＞0．

提示	示范
(1)本题可以求出`y=a^x`的反函数`y=text(log)_ax`，用逐个验证法选出答案.     (2)根据对数的性质，对字母a进行分类讨论．
解:(1)显然A、B选项不正确，因为text(log)_a1=0，其值不可能为1、2．     若M(2，3)在函数`y=a^x`的图象上，则`3=a^2`．     又M(2，3)在其反函数`y=text(log)_ax`的图象上，则`3=text(log)_a2`，此时a无解．     若N`(1/2，1/4)`在函数`y=a^x`的图象上，则`1/4=a^(1/2)`，解得`a=1/16`．     又N`(1/2，1/4)`在其反函数`y=text(log)_ax`的图象上，则`1/4=text(log)_a1/2`， 解得`a=1/16`，故N为公共点．     答案：D     (2)①显然，当a＞1时，不等式成立．当0＜a＜1时，由l`text(log)_a2/3＜1=text(log)_a a`，     得`0＜a＜2/3`．故所求a的取值范围为`0＜a＜2/3`或a＞1．     ②原不等式等价于`{(a＞1，),(0＜1-2a＜a):}`I或`{(0＜a＜1，),(1-2a＞a):}`II     由I得a∈`O/`；由II知`0＜a＜1/3`．     ∴`a∈(0，1/3)`．     ③原不等式等价于`{(a＞1，),(1-2a＞1):}`或`{(0＜a＜1，),(0＜1-2a＜1):}`．     解之，得`0＜a＜1/2`．     评注:(1)考查指数函数的图象和性质的高考题非常重要，要弄准记熟，并注意结合图象分析．     (2)由此类不等式确定a的取值范围，本质上是单调性的应用，但要注意对a的取值情况进行分类讨论．讨论的原因就是欲利用对数函数的单调性，将含对数的不等式，转化为代数不等式．

    3、(1)设`f(x)=text(lg)(1+2^x+4^x•a)/3`，其中`a∈R`，如果当`x∈(-∞，1]`时，f(x)有意义，求a的取值范围．
    (2)已知x满足不等式`2(text(log)_(1/2)x)^2+7text(log)_(1/2)x+3`≤0，求函数`f(x)=text(log)_2x/4•text(log)_2x/2`的最大值和最小值．

提示	示范
(1)本题可采用命题转化思想．f(x)有意义，必须`(1+2^x+4^x•a)/3＞0`，将原命题转化为不等式，再变形为`a＞-(1/4)^x-(1/2)^x`，进行转化为求指数函数的最值，最后转化为求指数函数的单调区间.     (2)运用对数函数的单调性以及求函数最值的方法先求出`text(log)_(1/2)x`的范围，再求f(x)的最值.
解:(1)∵`(1+2^x+4^x•a)/3＞0`，x∈(-∞，1],∴`a＞-(1/4)^x-(1/2)^x`,     当且仅当a大于`g(x)=-(1/4)^x-(1/2)^x`的最大值时，`a＞-(1/4)^x-(1/2)^x`恒成立．     而g(x)在R上是单调递增函数，又x∈(-∞，1]，     ∴当且仅当x=1时，g(x)的最大值为`-1/4-1/2=-3/4`．     ∴`a＞-3/4`．     (2)由`2(text(log)_(1/2)x)^2+7text(log)_(1/2)x+3`≤0     可解得-3≤`text(log)_(1/2)x`≤-`1/2`即sqrt(2)≤x≤8     ∴`1/2`≤`text(log)_2x`≤3     ∵`f(x)=(text(log)_2x-2)(text(log)_2x-1)=(text(log)_2x-3/2)^2-1/4`     ∴当`text(log)_2x=3/2`，即`x=2sqrt(2)`时，f(x)有最小值-`1/4`．     又当`text(log)_2x=3`，即x=8时，f(x)有最大值2.     ∴`f(x)_(min)=-1/4，f(x)_(max)=2`．     评注:(1)转化思想是一种重要的数学思想，掌握这种题型的解法，便会大幅度提升你的数学能力．解f(x)≥a(或f(x)≤a)在定义域内恒成立问题，通常都要求f(x)的最大值或最小值，从而转化为解不等式的问题．      (2)此类题目用配方法求最值，在求最值时要注意自变量的取值范围.

    学习感悟
    1、指数式、对数式的运算，求值、化简、证明等问题主要运用幂、对数的运算则及性质加以解决，在使用运算法则时要注意法则的逆用．在指数、对数的运算时还要注意相互间的转化．
    2、在分数指数幂的运算中，要注意公式变式使用，如`a^( 1/2)+b^( 1/2)=(a-b)/(a^( 1/2)-b^( 1/2)),a+b=(a^( 1/3)+b^( 1/3))[a^( 2/3)-a^( 1/3)*b^( 1/3)+b^( 2/3)]`等形式．
    3、比较大小的一般步骤：(1)先分类，即以O，1等为界数，把各数进行归类；(2)同类数中再找同底数、同指数、同真数借用函数的性质与图象进行比较，再复杂的，可用引入 中间量、作差、作商、换底等方法比较．
    4、对于指数函数、对数与其它函数的复合函数的定义域、值域、最值的运算，要注意用换元的思想去解决．
    5、对含参数的指数函数、对数函数研究单调性时，要注意对底分类讨论．解决对数问题时，首先要考虑定义域.