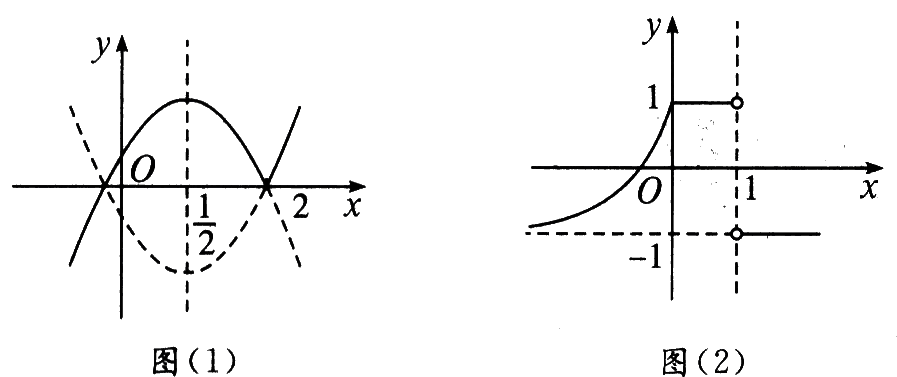|
一、复习目标 1、掌握基本初等函数的图象及用描点法作函数图象的步骤. 2、掌握函数图象的平移变换与对称变换. 3、会借助函数图象解决有关问题. 二、重点难点 难点:借助函数图象解决有关问题. 三、特别提示 |
|
知识梳理 |
|
应用举例 二、案例示范
1、作下列函数的图象:
2、设函数f(x)=`|x^2-4x-5|`. (1)在区间[-2,6]上画出函数f(x)的图象; (2)设集合`A={x|f(x)≥5}`,`B=(-∞,-2]uu[0,4]uu[6,+∞)`.试判断集合A和B之间的关系,并给出证明.
3、设函数f(x)=`x^2-2|x|-1`(-3≤x≤3). (1)证明f(x)是偶函数; (2)画出这个函数的图象; (3)指出函数f(x)的单调区间,并说明在各个单调区间上f(x)是增函数还是减函数;
|
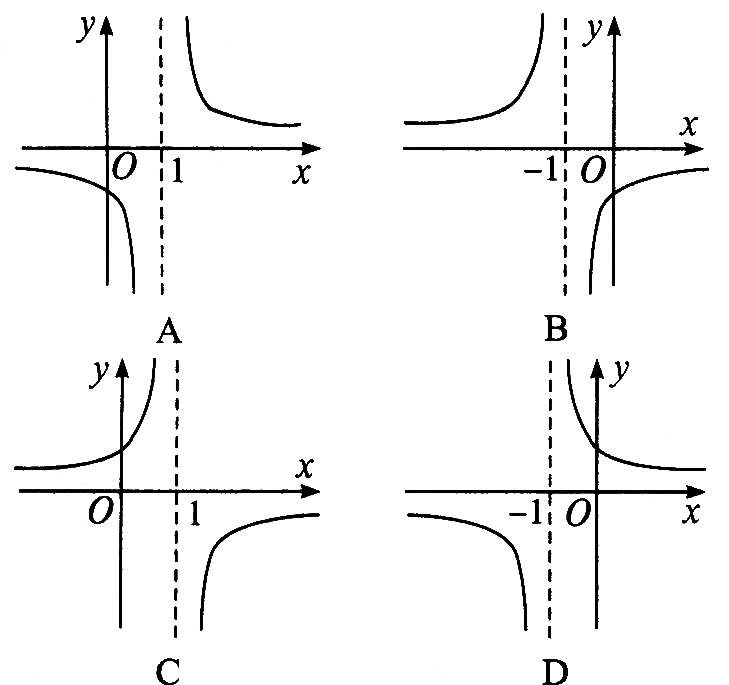
| 实践体验 (在实践中提高能力,在体验中反思感悟,力求独立,力求提高) 1、已知函数`f(x)=(x-1)/a(a>0且a≠1)`,在同一直角坐标系中,如图所示,`y=f^-1(x)与y=a^(|x-1|)`的图象可能是( ) 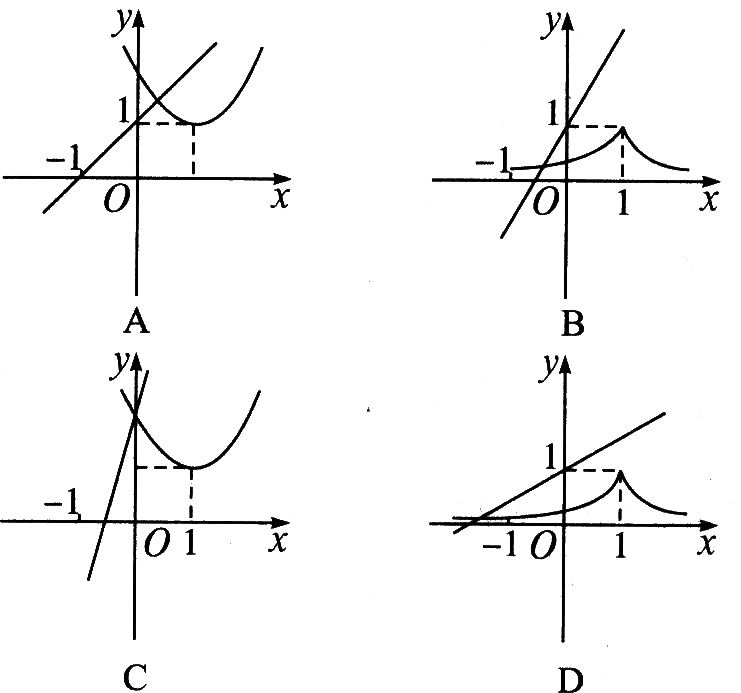
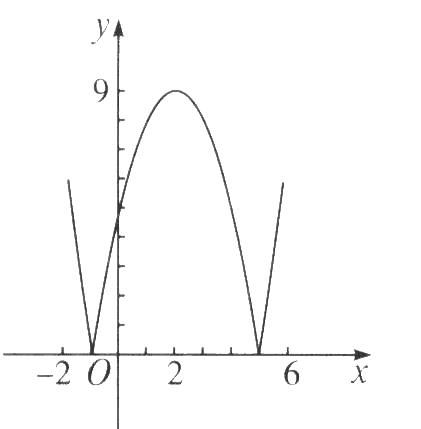
2、已知设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图所示,则不等式f(x)<0的解是____. 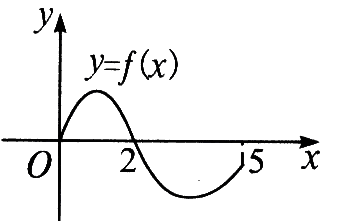
|
| 拓展探究 在同一平面直角坐标系中,函数y=f(x)和y=g(x)的图象关于直线y=x对称,现将y=g(x)的图象沿x轴向左平移2个单位,再沿y轴向上平移1个单位,所得到的图象是由两条线段组成的折线(如图),则函数f(x)的表达式为( ) 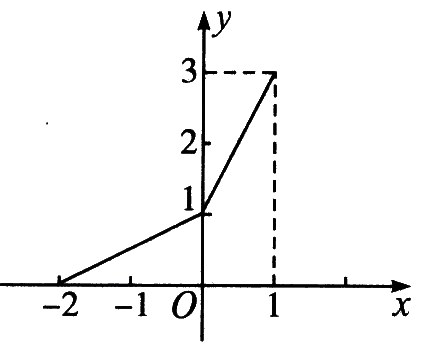 A.`f(x)={(2x+2text(, )-1<=x<=0),(x/2+2text(, )0<x<=2):}` B.`f(x)={(2x-2text(, )-1<=x<=0),(x/2-2text(, )0<x<=2):}` C.`f(x)={(2x-2text(, )1<=x<=2),(x/2+1text(, )2<x<=4):}` D.`f(x)={(2x-6text(, )1<=x<=2),(x/2-3text(, )2<x<=4):}`
|
|
|
|
|
学习感悟 |