2022年上海

面向未来，活在当下！

收藏夹
我的

当前：首页 > 数学 > 高考题 > 2022 > 2022年上海

2022年高考数学上海1（4分）已知

$z=1+i$ （其中

$i$ 为虚数单位），则

$2\overline{z}=$ ____．【答案详解】

2022年高考数学上海2（4分）双曲线

$\dfrac{x^2}{9}-y^{2}=1$ 的实轴长为____．
【答案详解】

2022年高考数学上海3（4分）函数

$f(x)=\cos ^{2}x-\sin ^{2}x+1$ 的周期为____．【答案详解】

2022年高考数学上海4（4分）已知

$a\in R$ ，行列式

$\vert {\left.\begin{array}{l}a&1\\ 3&2\end{array}\right.}\vert$ 的值与行列式

$\vert {\left.\begin{array}{l}a&0\\ 4&1\end{array}\right.}\vert$ 的值相等，则

$a=$ ____．
【答案详解】

2022年高考数学上海5（4分）已知圆柱的高为4，底面积为

$9\pi$ ，则圆柱的侧面积为____．
【答案详解】

2022年高考数学上海6（4分）

$x-y\leqslant 0$ ，

$x+y-1\geqslant 0$ ，求

$z=x+2y$ 的最小值 ____．
【答案详解】

2022年高考数学上海7（5分）二项式

$(3+x)^{n}$ 的展开式中，

$x^{2}$ 项的系数是常数项的5倍，则

$n=$ ____．
【答案详解】

2022年高考数学上海8（5分）若函数

$f(x)=\left\{\begin{array}{l}{{a}^{2}x-1}&{x < 0}\\ {x+a}&{x > 0}\\ {0}&{x=0}\end{array}\right.$ ，为奇函数，求参数

$a$ 的值为____．【答案详解】

2022年高考数学上海9（5分）为了检测学生的身体素质指标，从游泳类1项，球类3项，田径类4项共8项项目中随机抽取4项进行检测，则每一类都被抽到的概率为____．【答案详解】

2022年高考数学上海10（5分）已知等差数列

$\{a_{n}\}$ 的公差不为零，

$S_{n}$ 为其前

$n$ 项和，若

$S_{5}=0$ ，则

$S_{i}(i=0$ ，1，2，

$\ldots$ ，

$100)$ 中不同的数值有____个．【答案详解】

2022年高考数学上海11（5分）若平面向量

$\vert \overrightarrow{a}\vert =\vert \overrightarrow{b}\vert =\vert \overrightarrow{c}\vert =\lambda$ ，且满足

$\overrightarrow{a}\cdot \overrightarrow{b}=0$ ，

$\overrightarrow{a}\cdot \overrightarrow{c}=2$ ，

$\overrightarrow{b}\cdot \overrightarrow{c}=1$ ，则

$\lambda =$ ____．【答案详解】

2022年高考数学上海12（5分）设函数

$f(x)$ 满足

$f(x)=f(\dfrac{1}{x+1})$ ，定义域为

$D=[0$ ，

$+\infty )$ ，值域为

$A$ ，若集合

$\{y\vert y=f(x)$ ，

$x\in [0$ ，

$a]\}$ 可取得

$A$ 中所有值，则参数

$a$ 的取值范围为____．【答案详解】

2022年高考数学上海13（5分）若集合

$A=[-1$ ，

$2)$ ，

$B=Z$ ，则

$A\bigcap B=($ 　　)
A．

$\{-2$ ，

$-1$ ，0，

$1\}$ B．

$\{-1$ ，0，

$1\}$ C．

$\{-1$ ，

$0\}$ D．

$\{-1\}$ 【答案详解】

2022年高考数学上海14（5分）若实数

$a$ 、

$b$ 满足

$a > b > 0$ ，下列不等式中恒成立的是(　　)
A．

$a+b > 2\sqrt{ab}$ B．

$a+b < 2\sqrt{ab}$ C．

$\dfrac{a}{2}+2b > 2\sqrt{ab}$ D．

$\dfrac{a}{2}+2b < 2\sqrt{ab}$ 【答案详解】

2022年高考数学上海15（5分）如图正方体

$ABCD-A_{1}B_{1}C_{1}D_{1}$ 中，

$P$ 、

$Q$ 、

$R$ 、

$S$ 分别为棱

$AB$ 、

$BC$ 、

$BB_{1}$ 、

$CD$ 的中点，联结

$A_{1}S$ ，

$B_{1}D$ ．空间任意两点

$M$ 、

$N$ ，若线段

$MN$ 上不存在点在线段

$A_{1}S$ 、

$B_{1}D$ 上，则称

$MN$ 两点可视，则下列选项中与点

$D_{1}$ 可视的为(　　)

A．点

$P$ B．点

$B$ C．点

$R$ D．点

$Q$ 【答案详解】

2022年高考数学上海16（5分）设集合

$\Omega =\{(x$ ，

$y)\vert (x-k)^{2}+(y-k^{2})^{2}=4\vert k\vert$ ，

$k\in Z\}$
①存在直线

$l$ ，使得集合

$\Omega$ 中不存在点在

$l$ 上，而存在点在

$l$ 两侧；
②存在直线

$l$ ，使得集合

$\Omega$ 中存在无数点在

$l$ 上；(　　)
A．①成立②成立 B．①成立②不成立
C．①不成立②成立 D．①不成立②不成立【答案详解】

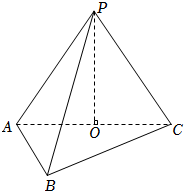
2022年高考数学上海17（14分）如图所示三棱锥，底面为等边

$\Delta ABC$ ，

$O$ 为

$AC$ 边中点，且

$PO\bot$ 底面

$ABC$ ，

$AP=AC=2$ ．
（1）求三棱锥体积

$V_{P-ABC}$ ；
（2）若

$M$ 为

$BC$ 中点，求

$PM$ 与面

$PAC$ 所成角大小．

【答案详解】

2022年高考数学上海18（14分）

$f(x)=\log _{3}(a+x)+\log _{3}(6-x)$ ．
（1）若将函数

$f(x)$ 图像向下移

$m(m > 0)$ 后，图像经过

$(3,0)$ ，

$(5,0)$ ，求实数

$a$ ，

$m$ 的值．
（2）若

$a > -3$ 且

$a\ne 0$ ，求解不等式

$f(x)\leqslant f(6-x)$ ．【答案详解】

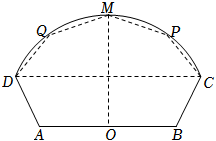
2022年高考数学上海19（14分）在如图所示的五边形中，

$AD=BC=6$ ，

$AB=20$ ，

$O$ 为

$AB$ 中点，曲线

$CD$ 上任一点到

$O$ 距离相等，角

$\angle DAB=\angle ABC=120^\circ$ ，

$P$ ，

$Q$ 关于

$OM$ 对称，

$MO\bot AB$ ；
（1）若点

$P$ 与点

$C$ 重合，求

$\angle POB$ 的大小；
（2）

$P$ 在何位置，求五边形面积

$S$ 的最大值．

【答案详解】

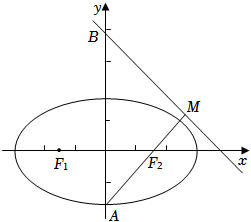
2022年高考数学上海20（16分）设有椭圆方程

$\Gamma :\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a > b > 0)$ ，直线

$l:x+y-4\sqrt{2}=0$ ，

$\Gamma$ 下端点为

$A$ ，

$M$ 在

$l$ 上，左、右焦点分别为

$F_{1}(-\sqrt{2}$ ，

$0)$ 、

$F_{2}(\sqrt{2}$ ，

$0)$ ．
（1）

$a=2$ ，

$AM$ 中点在

$x$ 轴上，求点

$M$ 的坐标；
（2）直线

$l$ 与

$y$ 轴交于

$B$ ，直线

$AM$ 经过右焦点

$F_{2}$ ，在

$\Delta ABM$ 中有一内角余弦值为

$\dfrac{3}{5}$ ，求

$b$ ；
（3）在椭圆

$\Gamma$ 上存在一点

$P$ 到

$l$ 距离为

$d$ ，使

$\vert PF_{1}\vert +\vert PF_{2}\vert +d=6$ ，随

$a$ 的变化，求

$d$ 的最小值．

【答案详解】

2022年高考数学上海21（18分）数列

$\{a_{n}\}$ 对任意

$n\in N^{*}$ 且

$n\geqslant 2$ ，均存在正整数

$i\in [1$ ，

$n-1]$ ，满足

$a_{n+1}=2a_{n}-a_{i}$ ，

$a_{1}=1$ ，

$a_{2}=3$ ．
（1）求

$a_{4}$ 可能值；
（2）命题

$p$ ：若

$a_{1}$ ，

$a_{2}$ ，

$\dotsb$ ，

$a_{8}$ 成等差数列，则

$a_{9} < 30$ ，证明

$p$ 为真，同时写出

$p$ 逆命题

$q$ ，并判断命题

$q$ 是真是假，说明理由；
（3）若

$a_{2m}=3^{m}$ ，

$(m\in N^{*})$ 成立，求数列

$\{a_{n}\}$ 的通项公式．【答案详解】

开心教练从2004年开始自费开设这个网站. 为了可以持续免费提供这些内容, 并且没有广告干扰，请大家随意打赏，谢谢！,
（微信中可直接长按微信打赏二维码。）

微信	支付宝