2022年高考数学上海6

（4分）

$x-y\leqslant 0$ ，

$x+y-1\geqslant 0$ ，求

$z=x+2y$ 的最小值　

$\dfrac{3}{2}$ 　．
分析：根据已知条件作出可行域，再求目标函数的最小值即可．
解：如图所示：

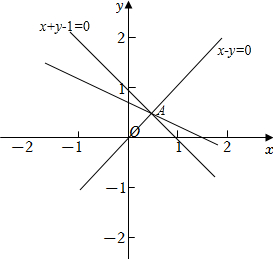
由

$x-y\leqslant 0$ ，

$x+y-1\geqslant 0$ ，可知行域为直线

$x-y=0$ 的左上方和

$x+y-1=0$ 的右上方的公共部分，
联立

$\left\{\begin{array}{l}{x-y=0}\\ {x+y-1=0}\end{array}\right.$ ，可得

$\left\{\begin{array}{l}{x=\dfrac{1}{2}}\\ {y=\dfrac{1}{2}}\end{array}\right.$ ，即图中点

$A(\dfrac{1}{2}$ ，

$\dfrac{1}{2})$ ，
当目标函数

$z=x+2y$ 沿着与正方向向量

$\overrightarrow{a}=(1,2)$ 的相反向量平移时，离开区间时取最小值，
即目标函数

$z=x+2y$ 过点

$A(\dfrac{1}{2}$ ，

$\dfrac{1}{2})$ 时，取最小值：

$\dfrac{1}{2}+2\times \dfrac{1}{2}=\dfrac{3}{2}$ ．
故答案为：

$\dfrac{3}{2}$ ．
点评：本题考查了线性规划知识，难点在于找到目标函数取最小值的位置，属于中档题．

相关知识

无相关信息

学习笔记（共有 0 条）