2022年高考数学新高考Ⅰ-8(5分)已知正四棱锥的侧棱长为$l$,其各顶点都在同一球面上.若该球的体积为$36\pi$,且$3\leqslant l\leqslant 3\sqrt{3}$,则该正四棱锥体积的取值范围是( )
A.$[18$,$\dfrac{81}{4}]$ B.$[\dfrac{27}{4}$,$\dfrac{81}{4}]$ C.$[\dfrac{27}{4}$,$\dfrac{64}{3}]$ D.$[18$,$27]$【答案详解】 |
2022年高考数学新高考Ⅰ-4(5分)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔$148.5m$时,相应水面的面积为$140.0km^{2}$;水位为海拔$157.5m$时,相应水面的面积为$180.0km^{2}$.将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔$148.5m$上升到$157.5m$时,增加的水量约为$(\sqrt{7}\approx 2.65)($ )
A.$1.0\times 10^{9}m^{3}$ B.$1.2\times 10^{9}m^{3}$ C.$1.4\times 10^{9}m^{3}$ D.$1.6\times 10^{9}m^{3}$【答案详解】 |
2021年高考数学新高考Ⅰ-20如图,在三棱锥$A-BCD$中,平面$ABD\bot$平面$BCD$,$AB=AD$,$O$为$BD$的中点.
(1)证明:$OA\bot CD$;
(2)若$\Delta OCD$是边长为1的等边三角形,点$E$在棱$AD$上,$DE=2EA$,且二面角$E-BC-D$的大小为$45^\circ$,求三棱锥$A-BCD$的体积.
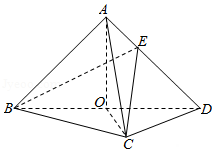 【答案详解】 【答案详解】 |
2021年高考数学新高考Ⅰ-12(5分)在正三棱柱$ABC-A_{1}B_{1}C_{1}$中,$AB=AA_{1}=1$,点$P$满足$\overrightarrow{BP}=\lambda \overrightarrow{BC}+\mu \overrightarrow{B{B}_{1}}$,其中$\lambda \in [0$,$1]$,$\mu \in [0$,$1]$,则( )
A.当$\lambda =1$时,△$AB_{1}P$的周长为定值
B.当$\mu =1$时,三棱锥$P-A_{1}BC$的体积为定值
C.当$\lambda =\dfrac{1}{2}$时,有且仅有一个点$P$,使得$A_{1}P\bot BP$
D.当$\mu =\dfrac{1}{2}$时,有且仅有一个点$P$,使得$A_{1}B\bot$平面$AB_{1}P$【答案详解】 |
2021年高考数学新高考Ⅰ-12(5分)在正三棱柱$ABC-A_{1}B_{1}C_{1}$中,$AB=AA_{1}=1$,点$P$满足$\overrightarrow{BP}=\lambda \overrightarrow{BC}+\mu \overrightarrow{B{B}_{1}}$,其中$\lambda \in [0$,$1]$,$\mu \in [0$,$1]$,则( )
A.当$\lambda =1$时,△$AB_{1}P$的周长为定值
B.当$\mu =1$时,三棱锥$P-A_{1}BC$的体积为定值
C.当$\lambda =\dfrac{1}{2}$时,有且仅有一个点$P$,使得$A_{1}P\bot BP$
D.当$\mu =\dfrac{1}{2}$时,有且仅有一个点$P$,使得$A_{1}B\bot$平面$AB_{1}P$【答案详解】 |

