数列 - 91学

活在当下，做最好的自己！

收藏夹
我的

当前：首页 > TAG信息列表 > 数列

2023年高考数学新高考Ⅱ-8（5分）记

$S_{n}$ 为等比数列

$\{a_{n}\}$ 的前

$n$ 项和，若

$S_{4}=-5$ ，

$S_{6}=21S_{2}$ ，则

$S_{8}=($ 　　

$)$
A．120 B．85 C．

$-85$ D．

$-120$ 【答案详解】

2023年高考数学新高考Ⅰ-20（12分）设等差数列

$\{a_{n}\}$ 的公差为

$d$ ，且

$d > 1$ ．令

$b_{n}=\dfrac{{n}^{2}+n}{{a}_{n}}$ ，记

$S_{n}$ ，

$T_{n}$ 分别为数列

$\{a_{n}\}$ ，

$\{b_{n}\}$ 的前

$n$ 项和．
（1）若

$3a_{2}=3a_{1}+a_{3}$ ，

$S_{3}+T_{3}=21$ ，求

$\{a_{n}\}$ 的通项公式；
（2）若

$\{b_{n}\}$ 为等差数列，且

$S_{99}-T_{99}=99$ ，求

$d$ ．【答案详解】

2023年高考数学新高考Ⅰ-7（5分）记

$S_{n}$ 为数列

$\{a_{n}\}$ 的前

$n$ 项和，设甲：

$\{a_{n}\}$ 为等差数列；乙：

$\{\dfrac{S_n}{n}\}$ 为等差数列，则

$($ 　　

$)$
A．甲是乙的充分条件但不是必要条件
B．甲是乙的必要条件但不是充分条件
C．甲是乙的充要条件
D．甲既不是乙的充分条件也不是乙的必要条件【答案详解】

2022年高考数学新高考Ⅱ-17（10分）已知

$\{a_{n}\}$ 是等差数列，

$\{b_{n}\}$ 是公比为2的等比数列，且

$a_{2}-b_{2}=a_{3}-b_{3}=b_{4}-a_{4}$ ．
（1）证明：

$a_{1}=b_{1}$ ；
（2）求集合

$\{k\vert b_{k}=a_{m}+a_{1}$ ，

$1\leqslant m\leqslant 500\}$ 中元素的个数．【答案详解】

2022年高考数学新高考Ⅱ-3（5分）图1是中国古代建筑中的举架结构，

$AA\prime$ ，

$BB\prime$ ，

$CC\prime$ ，

$DD\prime$ 是桁，相邻桁的水平距离称为步，垂直距离称为举．图2是某古代建筑屋顶截面的示意图，其中

$DD_{1}$ ，

$CC_{1}$ ，

$BB_{1}$ ，

$AA_{1}$ 是举，

$OD_{1}$ ，

$DC_{1}$ ，

$CB_{1}$ ，

$BA_{1}$ 是相等的步，相邻桁的举步之比分别为

$\dfrac{D{D_1}}{O{D_1}}=0.5$ ，

$\dfrac{C{C_1}}{D{C_1}}=k_{1}$ ，

$\dfrac{B{B_1}}{C{B_1}}=k_{2}$ ，

$\dfrac{A{A_1}}{B{A_1}}=k_{3}$ ．已知

$k_{1}$ ，

$k_{2}$ ，

$k_{3}$ 成公差为0.1的等差数列，且直线

$OA$ 的斜率为0.725，则

$k_{3}=($ 　　)

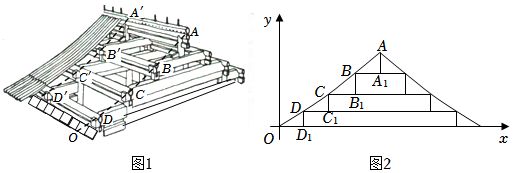
A．0.75 B．0.8 C．0.85 D．0.9【答案详解】

2022年高考数学新高考Ⅰ-17（10分）记

$S_{n}$ 为数列

$\{a_{n}\}$ 的前

$n$ 项和，已知

$a_{1}=1$ ，

$\{\dfrac{{S}_{n}}{{a}_{n}}\}$ 是公差为

$\dfrac{1}{3}$ 的等差数列．
（1）求

$\{a_{n}\}$ 的通项公式；
（2）证明：

$\dfrac{1}{a_1}+\dfrac{1}{a_2}+\ldots +\dfrac{1}{a_n} < 2$ ．【答案详解】

2021年高考数学新高考Ⅰ-17（10分）已知数列

$\{a_{n}\}$ 满足

$a_{1}=1$ ，

${{a}_{n+1}}=\left\{ \begin{array}{*{35}{l}} {{a}_{n}}+1,n, \\ {{a}_{n}}+2,n\cdot \\ \end{array} \right.$
（1）记

$b_{n}=a_{2n}$ ，写出

$b_{1}$ ，

$b_{2}$ ，并求数列

$\{b_{n}\}$ 的通项公式；
（2）求

$\{a_{n}\}$ 的前20项和．【答案详解】

2021年高考数学新高考Ⅰ-16某校学生在研究民间剪纸艺术时，发现剪纸时经常会沿纸的某条对称轴把纸对折．规格为

$20dm\times 12dm$ 的长方形纸，对折1次共可以得到

$10dm\times 12dm$ ，

$20dm\times 6dm$ 两种规格的图形，它们的面积之和

$S_{1}=240dm^{2}$ ，对折2次共可以得到

$5dm\times 12dm$ ，

$10dm\times 6dm$ ，

$20dm\times 3dm$ 三种规格的图形，它们的面积之和

$S_{2}=180dm^{2}$ ，以此类推．则对折4次共可以得到不同规格图形的种数为____；如果对折

$n$ 次，那么

$\sum\limits_{k=1}^{n}S_{k}=$ ____

$dm^{2}$ ．【答案详解】

2020年高考数学新高考Ⅱ-18（12分）已知公比大于1的等比数列

$\{a_{n}\}$ 满足

$a_{2}+a_{4}=20$ ，

$a_{3}=8$ ．
（1）求

$\{a_{n}\}$ 的通项公式；
（2）求

$a_{1}a_{2}-a_{2}a_{3}+\ldots +(-1)^{n-1}a_{n}a_{n+1}$ ．【答案详解】

2020年高考数学新高考Ⅱ-15将数列

$\{2n-1\}$ 与

$\{3n-2\}$ 的公共项从小到大排列得到数列

$\{a_{n}\}$ ，则

$\{a_{n}\}$ 的前

$n$ 项和为____．【答案详解】

2020年高考数学全国卷Ⅲ--文17(2020全国Ⅲ卷计算题)设等比数列满足，。（1）求的通项公式。（2）记为数列的前项和，若，求。【出处】2020年普通高等学校招生全国统一考试（新课标Ⅲ卷）：文数第17题【答案】（1）设等比数列公比为，则解得，，所以。（2），所以，所以，，，若，则，即，即，因为为正整【答案详解】

2020年高考数学全国卷Ⅱ--文14(2020全国Ⅱ卷其他)记为等差数列的前项和，若，，则_____。【出处】2020年普通高等学校招生全国统一考试（新课标Ⅱ卷）：文数第14题【答案】【解析】本题主要考查等差数列。在等差数列中，，设公差为，所以，，所以，又因为，所以，所以，所以。故【答案详解】

2020年高考数学全国卷Ⅱ--文6(2020全国Ⅱ卷单选题)记为等比数列的前项和。若，，则（）。【A】【B】【C】【D】【出处】2020年普通高等学校招生全国统一考试（新课标Ⅱ卷）：文数第6题【题情】本题共被作答5076次，正确率为56.97%，易错项为C【解析】本题主要考【答案详解】

2020年高考数学全国卷Ⅰ--文16(2020全国Ⅰ卷其他)数列满足，前项和为，则_____。【出处】2020年普通高等学校招生全国统一考试（新课标Ⅰ卷）：文数第16题【答案】【解析】本题主要考查数列的递推与通项和数列的求和。当为偶数时，，所以，因为前项和为，所以，当为奇【答案详解】

2020年高考数学全国卷Ⅰ--文10(2020全国Ⅰ卷单选题)设是等比数列，且，，则（）。【A】【B】【C】【D】【出处】2020年普通高等学校招生全国统一考试（新课标Ⅰ卷）：文数第10题【题情】本题共被作答13372次，正确率为64.02%，易错项为B【解析】本题主要考查等比数【答案详解】

2020年高考数学浙江20(2020浙江卷计算题)已知数列，，中，，，，。（1）若数列为等比数列，公比，且，求的值与数列的通项公式。（2）若数列为等差数列，公差，证明：，。【出处】2020年普通高等学校招生全国统一考试（浙江卷）：数学第20题【答案】（1）因为为等比数列，且，所以，即，整理得，【答案详解】

2020年高考数学浙江11(2020浙江卷其他)已知数列满足，则_____。【出处】2020年普通高等学校招生全国统一考试（浙江卷）：数学第11题【答案】【解析】本题主要考查数列的概念与表示。因为满足（），所以，，，所以。故本题正确答案为。【考点】数列的通项与递【答案详解】

2020年高考数学浙江7(2020浙江卷单选题)已知等差数列的前项和为，公差，。记，，。下列等式不可能成立的是（）。【A】【B】【C】【D】【出处】2020年普通高等学校招生全国统一考试（浙江卷）：数学第7题【题情】本题共被作答997次，正确率为42.73%，易错项【答案详解】

2020年高考数学江苏20(2020江苏卷计算题)已知数列（）的首项，前项和为。设和为常数，若对一切正整数均有成立，则称此数列为“”数列。（1）若等差数列是“”数列，求的值。（2）若数列是“”数列，且，求数列的通项公式。（3）对于给定的，是否存在三个不同的数列为“【答案详解】

2020年高考数学江苏11(2020江苏卷其他)设是公差为的等差数列，是公比为的等比数列，已知的前项和（），则的值是_____。【出处】2020年普通高等学校招生全国统一考试（江苏卷）：理数第11题【答案】【解析】本题主要考查等差数列、等比数列和数列的概念与【答案详解】

2020年高考数学天津19(2020天津卷计算题)已知为等差数列，为等比数列，，，。（1）求和的通项公式。（2）记的前项和为，求证：（）。（3）对任意的正整数，设。求数列的前项和。【出处】2020年普通高等学校招生全国统一考试（天津卷）：数学第19题【答案】（1）因为为等差数列，，设公【答案详解】

2020年高考数学上海21(2020年上海卷计算题)有限数列，若满足，是项数，则称满足性质。（1）判断数列，，，和，，，，是否具有性质，请说明理由。（2）若，公比为的等比数列，项数为，具有性质，求的取值范围。（3）若是，，，的一个排列（），（，，，），，都具有性质，求所有满足条件的。【出处】2020年普通高【答案详解】

2020年高考数学上海8(2020年上海卷其他)已知是公差不为零的等差数列，且，则_____。【出处】2020年普通高等学校招生全国统一考试（上海卷）：数学第8题【答案】【解析】本题主要考查等差数列。设等差数列的公差为（），因为，所以，所以，所以，所以。故本题正确【答案详解】

2020年高考数学新高考Ⅰ-18(2020新高考Ⅰ卷计算题)已知公比大于的等比数列满足，。（1）求的通项公式。（2）记为在区间（）中的项的个数，求数列的前项和。【出处】2020年普通高等学校招生全国统一考试（新高考Ⅰ卷）：数学第18题【答案】（1）设的公比为，，因为，，所以，整理得，【答案详解】

2020年高考数学新高考Ⅰ-14(2020新高考Ⅰ卷其他)将数列与的公共项从小到大排列得到数列，则的前项和为_____。【出处】2020年普通高等学校招生全国统一考试（新高考Ⅰ卷）：数学第14题【答案】【解析】本题主要考查数列的求和。由题意可知的项是连续的【答案详解】

44 1 2 下一页尾页

开心教练从2004年开始自费开设这个网站. 为了可以持续免费提供这些内容, 并且没有广告干扰，请大家随意打赏，谢谢！,
（微信中可直接长按微信打赏二维码。）

微信	支付宝