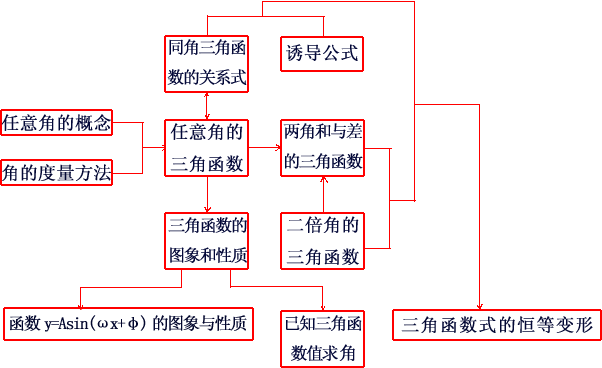
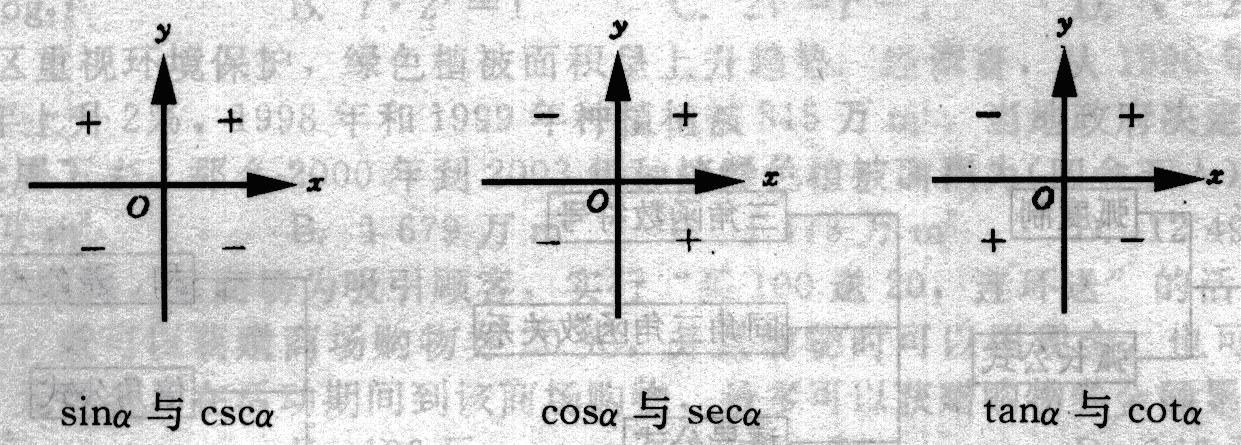
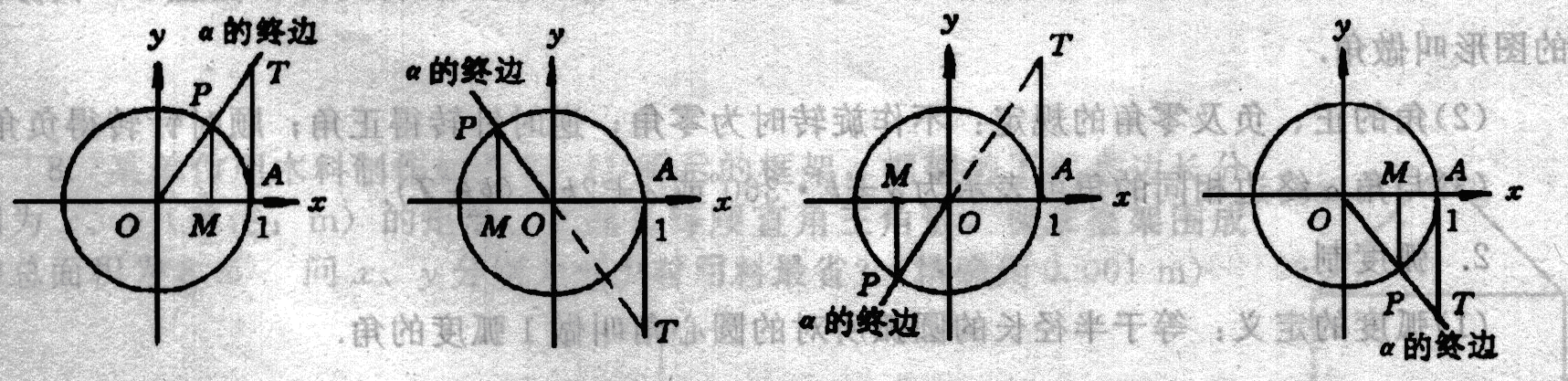
一、高考大纲
考试内容:
角的概念的推广、弧度制。
任意角的三角函数,单位圆中的三角函数线,同角三角函数的基本关系式:`sin^2alpha+cos^2alpha=1`,`sinalpha/cosalpha=tanalpha`,`tanalpha·cotalpha=1`,正弦、余弦的诱导公式。
两角和与差的正弦、余弦、正切,二倍角的正弦、余弦、正切。
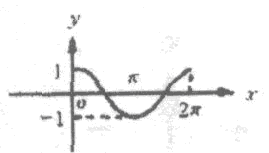
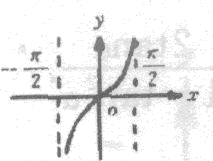
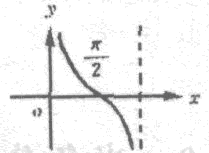
正弦函数、余弦函数的图像和性质。周期函数。函数`y=Asin(omegax+varphi)`的图像。正切函数的图像和性质。已知三角函数求角。
正弦定理。余弦定理。斜三角形解法。
考试要求:
(1)理解任意角的概念、弧度的意义。能正确地进行弧度与角度的换算。
(2)理解任意角的正弦、余弦、正切的定义。了解余切、正割、余割的定义,掌握同角三角函数的基本关系式。掌握正弦、余弦的诱导公式。了解周期函数与最小正周期的意义。
(3)掌握两角和与两角差的正弦、余弦、正切公式。掌握二倍角的正弦、余弦、正切公式。
(4)能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明。
(5)理解正弦函数、余弦函数、正切函数的图像和性质,会用“五点法”画正弦函数、余弦函数和函数`y=``Asin(omegax+varphi)`的简图,理解`A、omega、varphi`的物理意义。
(6)会由已知三角函数值求角,并会用符号`arcsinx、arc cosx、arctanx`表示。
(7)掌握正弦定理、余弦定理,并能初步运用它们解斜三角形。
二、高考要览
| 考试内容 |
能力层次 |
高考要求 |
考题年份分值 |
| 三角函数 |
掌握 |
任意角的正弦、余弦、正切的定义,用三角函数线表示正弦、余弦和正切;同角三角函数的基本关系式;正弦、余弦的诱导公式 |
|
2004 |
2005 |
2006 |
2007 |
2008 |
| |
全国Ⅲ.5 |
|
|
|
| |
全国Ⅰ.5 |
|
|
|
| 浙江.5 |
|
|
|
|
| 重庆.5 |
|
|
|
|
| 辽宁.5 |
|
|
|
|
| 北京春.5 |
|
|
|
|
| 安徽春.5 |
|
|
|
|
| 湖北.4 |
|
|
|
|
| |
|
湖北3.5 |
|
|
| |
|
陕西6.5 |
|
|
| 上海.5 |
|
上海6.4 |
|
|
| |
|
北京15.12 |
|
|
| 广东.12 |
|
广东15.14 |
|
|
|
和差倍
公式 |
掌握 |
通过公式的推导,了解它们的内在联系,从而培养逻辑推理能力. |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| 全国Ⅲ3.12 |
全国Ⅲ3.5 |
|
|
|
| |
全国Ⅱ.4 |
全国Ⅱ10.5 |
|
|
| |
浙江.12 |
浙江6.5 |
|
|
| 福建.5 |
福建.12 |
福建3.5 |
|
|
| |
|
陕西13.4 |
|
|
| |
|
江西14.4 |
|
|
| |
重庆.4 |
重庆13.4 |
|
|
| |
|
四川17.12 |
|
|
| 上海.4 |
|
|
|
|
| |
|
安徽17.12 |
|
|
| 江苏.12 |
江苏.5 |
|
|
|
| |
北京.4 |
|
|
|
| 天津.12 |
天津.12 |
|
|
|
| 湖南.12 |
|
|
|
|
| 湖北.12 |
|
|
|
|
| 北京春.4 |
北京春.5 |
|
|
|
|
| 图象与
性质
|
掌握 |
会用三角函数线画正弦函数,正弦函数的图象,由诱导公式画余弦函数的图象;理解它们的性质;会用“五点法” |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| |
全国Ⅲ.5 |
|
|
|
| |
|
全国Ⅱ2.5 |
|
|
| |
|
安徽8.12 |
|
|
| |
|
浙江15.12 |
|
|
| |
|
福建.12 |
|
|
| 北京.5 |
北京春.5 |
|
|
|
| 天津.5 |
|
|
|
|
|
| `y=Asin(omegax+varphi)`的图象 |
理解 |
`A、omega、varphi`的物理意义 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| |
全国Ⅰ.5 |
全国Ⅰ5.5 |
|
|
| |
全国Ⅱ.12 |
|
|
|
| |
全国Ⅲ.5 |
|
|
|
| 江苏.5 |
|
江苏4.5 |
|
|
| |
|
四川5.5 |
|
|
| 天津.5 |
天津.5 |
天津8.5 |
|
|
| |
福建.5 |
福建9.5 |
|
|
| |
|
安徽6.5 |
|
|
| |
山东.5 |
山东17.12 |
|
|
| 辽宁.5 |
|
辽宁17.12 |
|
|
| |
江西.5 |
|
|
|
| 北京.5 |
北京.5 |
|
|
|
| |
上海.5 |
|
|
|
| 广东.5 |
广东.5 |
|
|
|
| 湖北.5 |
|
|
|
|
|
| 掌握 |
用五点法”画函数`y=Asin(omegax+varphi)`的简图 |
| 三角最值 |
掌握 |
利用三角知识求最值 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| 全国Ⅰ.12 |
全国Ⅰ.5 |
|
|
|
| 全国Ⅲ.4 |
|
|
|
|
| |
|
辽宁11.5 |
|
|
| 重庆.12 |
重庆.12 |
重庆17.13 |
|
|
| |
江西.5 |
|
|
|
| 广东.5 |
|
|
|
|
|
| 应用 |
掌握 |
运用所学三角知识解决实际问题 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| |
|
全国Ⅰ17.12 |
|
|
| |
全国Ⅱ.5 |
全国Ⅱ17.12 |
|
|
| |
辽宁.12 |
|
|
|
| |
湖北.5 |
|
|
|
| |
湖南.5 |
|
|
|
|
三、命题趋势
近几年本章考查呈现以下特点:
1、题型和题量:选择题(或填空题)+解答题,保持一大一小(选择题较多,填空题主要是辽宁、北京、上海等地考查,且较少),分值16`~`17分,解答题多安排在第一道大题的位置.
2、知识点考查:集中于任意角的三角函数、同角基本关系式、诱导公式、和差倍半公式与图象和性质(含`y=` `Asin(omegax+varphi)`型及单调性、奇偶性、周期性、三角变换等)考查.其中,和、差、倍、半公式,图象和性质是常考常新,不避讳难点、热点问题.试题中与导数、向量的结合已成为各地试题中共同创新模式,和圆锥曲线结合主要体现出曲线参数方程的应用. `Asin(omegax+varphi)`型及单调性、奇偶性、周期性、三角变换等)考查.其中,和、差、倍、半公式,图象和性质是常考常新,不避讳难点、热点问题.试题中与导数、向量的结合已成为各地试题中共同创新模式,和圆锥曲线结合主要体现出曲线参数方程的应用.
3、难度与创新:三角函数试题以基本题为主,难度未超过中等,大多是容易题,即便和向量、不等式(最值)等知识综合,难度也偏低,仅2005年辽宁卷填空题可称得上是中等难度题,主要体现在角的配凑、公式的选择、方程思想方法的运用上.2006年2005年湖北卷理7、9利用三角函数线知识求解,在近几年高考中尚不多见;后者与江西卷理T18等作为导数(三角函数的导数)的应用是不错的创新尝试!同时也开创了三角与导数结合的先例.上海卷、江西卷2005年均出现三角分段函数和方程结合的题型,也对三角考查进行了良好的探索,尤其值得关注的是2005年湖南年卷理T15、天津卷理T22,均为创新的先锋,前者是新定义新情景问题,后者则放在压轴题,和导数、数列综合.2006年三角试题基本上难度在中等以下.
四、复习建议
本章知识虽不是高中数学重点内容,但在代数中很重要,是高中数学中课时量最大的一章,是高考必考的内容,试题大部分与三角函数的图象有关,三角函数的不等式,三角函数的最值、对称问题,周期问题都与三角函数的图象有关,学习本章首先要掌握三角函数图象,重点是`y=Asin(omegax+varphi)`图象(包括“五点法”作图)
分析近几年高考试题,重点围绕对三角函数图象与性质的考查,近几年高考试题与特点如下:
1、考小题重基础:有关三角函数的小题其考查重点在于基础知识,解析式、图象与图象变换、两域(定义域、值域以及最值)、四性(单调性、奇偶性、对称性、周期性)、反函数以及简单的三角变换(求值、化简及比较大小)
2、考大题难度明显降低:有关三角函数的大题即解答题,通过公式变形、转换来考查思维能力的题目已没有了,而是考查基本知识、基本技能与方法.
3、考应用题融入三角形中:既能考查解三角形的知识与方法,又能考查运用三角公式进行恒等变换的技能,备受命题者青睐.主要解法是充分利用三角形内角和定理、正(余)弦定理、面积公式等,并结合三角公式进行三角变换.
4、考综合题体现三角的工具作用:由于近年高考题突出能力立意,加强对知识性和应用性的考查,故常常是在知识的交汇点出题,而三角知识是基础的基础,故考查与立体几何、解析几何等综合性问题时突出三角的工具作用.
三角函数作为历年高考中基础知识结构中不可或缺的重点内容之一.考查主要分成这样几大块:
(1)三角函数的概念,同角三角函数的关系,诱导公式.
(2)和、差、倍、半公式.
(3)三角函数的图象与性质(含`y=Asin(omegax+varphi)`型的图象、周期性、单调性、奇偶性等.
(4)三角函数性质的综合应用.
针对考试特点,复习汇总应做到:
1、准确定位,注重基础,学会通性通法,熟记公式
三角函数复习应和高考中的定位一致,既然是基础题居多,则必须紧紧抓住基础知识,落实好诱导公式,和、差倍、半等基本公式.
记忆三角函数的象限符号和切割化弦,辅助角公式(即`asintheta+bcostheta=root()(a^2+b^2)sin(theta+varphi)`)等最基本内容.
 注意正、余弦、正切的图象特征,抓住基本函数`y=sinx`,`y=cosx`,`y=tanx`等的特点(如单调区间、周期性、对称性等). 注意正、余弦、正切的图象特征,抓住基本函数`y=sinx`,`y=cosx`,`y=tanx`等的特点(如单调区间、周期性、对称性等).
注意公式的应用(化简、求值、证明)中三角变换的基本方法和技巧,降次(升幂)的基本原理,和“1”的化简巧用.
2、三角函数的图象与性质是重点训练内容
三角函数的图象和性质涉及到众多的知识点、考点.如定义域、值域、最值,图象变换中周期、相位、振幅等的变化技巧,单调性、奇偶性及对称性等诸多性质无不和图象联系密切,“五点
法”中起始点的选择等均十分关键,在用图象变换时,提倡先平移后压缩或伸展,但如果先压缩后平移(这经常出现于试题中),一定要先将x的系数提出来,使变化(平移)的大小是自变量x发生了多大变化,而不是变量整体上变了多少.涉及到符合函数的单调性问题,也必须注意对自变量的系数有效处理.
综上,学好三角函数应立足于基础,加强训练,熟记公式,加大题量训练,以题组与变式训练相结合,做到熟能生巧,综合运用,提高应试能力,同时,适当与其他知识(如平面向量、平面几何、解析几何、导数、数列、不等式、最值等)综合,做到以熟应变,以基础扎实的不变应对各种创新与变化.
五、思想与方法综览
1、数形结合思想
[案例1]关于`x`的方程`sinx+root()(3)cosx+a=0`在区间`[0,2pi]`上有且只有两不同的实根
(1)求实数`a`的范围;
(2)求这两个实根的和.
 分析:本题将方程转化为`sin(x+pi/3)=-a/2`的形式后,作出等号两边对应函数`t=sin(x+pi/3)`,`x∈[0,2pi]`及`y=-a/2`要的图象,观察图象交点个数问题.
分析:本题将方程转化为`sin(x+pi/3)=-a/2`的形式后,作出等号两边对应函数`t=sin(x+pi/3)`,`x∈[0,2pi]`及`y=-a/2`要的图象,观察图象交点个数问题.
解:(1)如图,原方程为`sin(x+pi/3)=-a/2`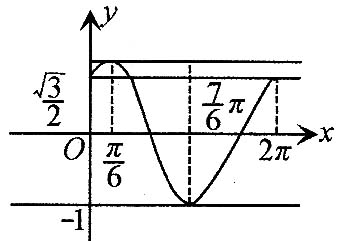 
方程在`[0,2pi]`上有两个相异实根的充要条件是
`{(-1<-a/2<1),(-a/2!=root()(3)/2):}`
即`-2<a<-root()(3)`或`-root()(3)<a<2`
(2)当`-2<a<-root()(3)`时
`root()(3)/2<-a/2<1`
设方程的一根为`x_1=pi/6+b`
则另一根为`x_2=pi/6-b`
∴`x_1+x_2=pi/3`
当`-root()(3)<a<2`时,`-1<-a/2<root()(3)/2`
设方程的一根为`x_1=(7pi)/6+b`,则另一根为`x_1=(7pi)/6-b`
∴`x_1+x_2=(7pi)/3`
2、分类讨论思想
[案例2]函数`y=sin^2x+acosx+5/8a-3/2(0≤x≤pi/2)`的最大值为1,求`a`的值.
分析:求三角函数值域或研究与最值有关的题目,也应化成一个角的三角函数,还应注意函数定义域对函数值域的影响,对含有字母的题目,仍然要注重分类讨论.
解:`y=sin^2x+acosx+5/8a-3/2`
= `-cos^2x+acosx+5/8a-1/2`
= `-(cosx-a/2)^2+(a^2)/4+5/8a-1/2`
令`t=cosx`,则`y=-(t-a/2)^2+(a^2)/4+5/8a-1/2`
由`0≤x≤pi/2知0≤t≤1`
①如果`0≤a/2≤1`,则`t=a/2`时,`y_(最大值)=(a^2)/4+5/8a-1/2`
由题意`(a^2)/4+5/8a-1/2=1`,得`a=-4`,或`a=3/2`
这两个值中只有`a=3/2`适合`0≤a/2≤1`
②如果`a/2<0`,则`t=0`时,`y_(最大值)=5/8a-1/2`
由`5/8a-1/2=1`得`a=12/5`,但它不适合`a/2<0`
③如果`a/2>1`,则`t=1`时,`y_(最大值)=13/8a-3/2`
由`13/8a-3/2=1`
∴`a=20/13`,但它不适合`a/2>1`
综合上述,`a=3/2` 
3、换元的思想
[案例3](2005·福建)设`a、b∈RR`,`a^2+2b^2=6`,则`a+b`的最小值是( )
A.`-2root()(2)`
B.`-5root()(3)/3` C.`-3`
D.`-7/2`
解:由`a^2+2b^2=6`,可设`a=root()(6)sinx`,`b=root()(3)cosx`,`x∈[0,2pi)`
则`a+b=root()(6)sinx+root()(3)cosx=3sin(x+varphi)`,其中`tanvarphi=root()(2)/2`
∴`(a+b)_(min)=-3`
4、方程的思想.
[案例4]一个直角三角形的三个内角的正弦值成等比数列,其最小内角是( )
A.`arc cos(root()(5)/2)`
B.`arcsin((root()(5)-1)/2)` C.`arc cos((1-root()(5))/2)` D.`arcsin((1-root()(5))/2)` 
解:设三角形三内角由小大到为:`alpha,90°-alpha,90°`
在`(0,pi/2]`内,`y=sinx`是增函数.
∴`sinalpha<sin(90°-alpha)<sin90°`
根据题意,得
`sin^2(90°-alpha)=sinalphasin(90°)`,即`sin^2alpha+sinalpah-1=0`
解得`sinalpha=(root()(5)-1)/2`
∴`a=arcsin((root()(5)-1)/2)`
答案:B.
5、化归与转化思想
[案例5]已知函数`f(x)=2sinx`,对任意的`x∈RR`都有`f(x_1)≤f(x)≤f(x_2)`,则`|x_1-x_2|`的最小值为(
)
A.`pi/4` B.`pi/2` C.`pi` D.`2pi`
解答:弄清楚题目的含义,不等式`f(x_1)≤f(x)≤f(x_2)`是什么适宜.
不难发现`f(x_1)、f(x_2)`分别为`f(x)`的最小值和最大值.
∵`f(x)=2sinx`的周期为`2pi`,
∴`|x_1-x_2|`的最小值`pi`.
答案:C
|