二、重点难点
    重点:任意角的概念, 弧度与角度的换算, 任意角的正弦、余弦、正切的定义及应用.

    难点:任意角的正弦、余弦、正切的定义及应用.

    三、特别提示
    1、角的集合的表示形式不是唯一的，如，终边在`y`轴的负半轴上的角的集合可用如下两种形式来表示：`{x|x=2kpi-pi/2，k∈ZZ}`，`{x|x=2kpi+(3pi)/2，k∈ZZ)`，但应注意角度制与弧度制不能混用，
    如：`{x|x=2kpi+270°，k∈ZZ}`是错误形式；
    角的概念推广及弧度制的建立，使角的集合与实数集`RR`之间建立了一个一一对应关系，使运算更为方便．
  2、三角函数中，角和三角函数值的对应关系是多值对应关系，即给定一个角，它的三角函数值是唯一确定的(除不存在的情况)；反过来，给定一个三角函数值，有无穷多个角和它对应．
  3、利用定义求三角函数值时，要注意角的终边所在的象限．当终边所在的象限不定时，要注意分情况讨论，分类讨论的思想是解决这类题的重要思想方法．
    4、注意第一象限角、锐角、小于90°的角的区别与联系．
  第一象限的角可以表示成`{alpha|k•360°<alpha<k•360°+90°，k∈ZZ}`，它包含锐角．锐角可以写成`{alpha| 0°<alpha<90°}`，它是第一象限的角．小于`90°`的角可以表示成`{alpha|alpha<90°}`，它包含锐角、零角及负角．
  5、单位圆中的三角函数线是数形结合的有效工具，借助它，不但可以画出准确的三角函数图象，还可以讨论三角函数性质．三角函数线是有向线段，字母顺序不能随意调换，当角`alpha`的终边与`x`轴重合时，正弦线、正切线分别变成一个点，此时角a的正弦值和正切值都为0；当角`alpha`的终边与`y`轴重合时，余弦线变成一个点，正切线不存在．

  1、任意角的概念：角可以看成是一条射线，绕着端点旋转而成的图形．开始位置的射线叫始边，终止位置的射线叫终边．规定按逆时针方向旋转所成的角为 正角，按顺时针方向旋转所成的角为负角，没有旋转的角为零角．

  2、象限角与轴上角：角的顶点与原点重合，角的始边与`x`轴重合，那么角的终边在第几象限，就说这个角是第几象限的角；如果角的终边在坐标轴上，这样的角叫轴上角，不属于任何象限．

    3、终边相同的角：若`alpha`为任意角，则与`alpha`终边相同的角，连同`alpha`在内，可以表示成`S={beta|beta=alpha+k·360°}`，`(k∈ZZ)`
    二、弧度制
    1、概念：把长度等于半径长的弧所对的圆心角叫做1弧度的角．用“弧度”作为单位来度量角的单位制叫弧度制，它的单位符号是`rad`，读作弧度．

    2、弧长公式与扇形面积公式：在弧度制下，弧长`l=|alpha|·r`(`r`为半径)，扇形面积`S_(扇形)`=`1/2lR=1/2R^2|alpha|`．
    3、弧度与角度的换算公式：180°=`pirad`，`1°=pi/180rad`，`1rad=(180/pi)°~~57.30°
    4、特殊角的角度数与弧度数的换算表：

    三、任意角的三角函数
    1、定义：在角`alpha`的终边上任取一点`P(x，y)`，设`|OP|=r(r>0)`，
   
    则`sinalpha=y/r`；`cosalpha=x/r`；`tanalpha=y/x`；`cotalpha=x/y`；`secalpha=r/x`；`cscalpha=r/y`

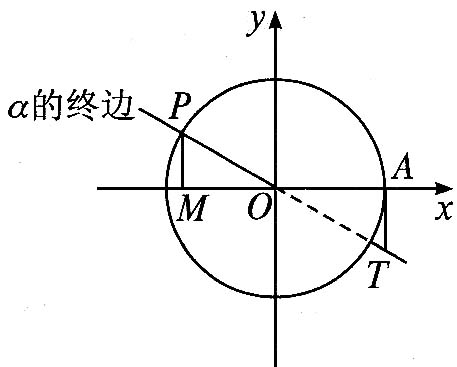
    2、三角函数线：如图，单位圆中的有向线段：`MP`、`OM`、`AT`分别叫做`alpha`的正弦线、余弦线、正切线．
    3、三角函数的定义域：`y=sinalpha`，`y=cosalpha`的定义域是`(-oo，+oo)`；
    `y=tanalpha`，`y=secalpha`的定义域是`{alpha|alpha!=pi/2+kpi，kinZ}`；
    `y=cotalpha`，`y=cscalpha`的定义域是`{alpha|alpha!=kpi，kinZ}`
    4、三角函数值在各象限中的符号  

    应用举例
    一、应用特点
    1、三角函数的概念的应用
    2、三角函数的符号判断
    3、弧长公式、扇形面积公式的应用

    1、`C`是曲线`y=root()(1-x^2)(-1<=x<=0)`上一点，`CD_|_y`轴，`D`是垂足，`A`点坐标是`(-1，0)`，`∠CAO=theta`(其中`O`为原点)，将`AC+CD`表示成关于`theta`的函数`f(theta)`，则`f(theta)`等于(   )
    A.`2costheta-cos2theta`      B.`costheta+sintheta`   

    C.`2costheta(1+costheta)`    D.`2sintheta+costheta-root()(2)`

提示	示范
运用三角函数的定义，明确`y=root()(1-x^2)(-1<=x<=0)`是`1/4`个半圆．
解:如下图`y=root()(1-x^2)`．     表示`1/4`个圆，连结`OC`．过`O`作`OM_|_AC`于`M`，由`OA=OC=1`，得`∠COA=pi-2theta`．     ∴`AC=2AM=2costheta`．又`∠COD=pi/2-∠COA=2theta-pi/2`．     ∴`CD=OCsin(2theta-pi/2)=-cos2theta`．     ∴`AC+CD=2costheta- cos2theta`．     答案：A     评注:(内容)

提示	示范
利用正、余弦，正、余切函数在各象限的符号．
解:(1)∵`sinthetain[-1，1]`、`costhetain[-1，1]`且`tantheta、cottheta`在同一象限内同号，故`theta`在第一或第三象限．     (2)`alpha`分四个象限讨论：     当`alpha`是一象限角时，`y=4`；当`alpha`是二象限角时，`y=-2`；     当`alpha`是三象限角时，`y=0`；当`alpha`是四象限角时，`y=-2`．     因此`y∈{-2，0，4}`．     评注:三角函数的自变量可以是角度制和弧度制，而弧度制可视为实数 ，因此要注意变量的双重性．

提示	示范
利用扇形的弧长公式和面积公式计算．
解:设扇形的圆心角是`thetarad`，因为扇形的弧长是`rtheta`，所以扇形的周长是`2r+rtheta`     依题意，得`2r+rtheta=pir`     ∵`theta=pi-2=(pi-2)xx(180/pi)°≈1.141xx57.30°≈65.32°≈65°19'`     ∴扇形的面积为`S=1/2r^2theta=1/2(pi-2)r^2`.     评注:在弧长公式`l=R|alpha|`，扇形面积公式`S=1/2lR=1/2R^2|alpha|`中，`alpha`是弧度．

    实践体验
    (在实践中提高能力，在体验中反思感悟，力求独立，力求提高)

    1、(1)写出终边在`y`轴上的角的集合；
    (2)若角`alpha`的终边和函数`y=-|x|`的图象重合，试写出角`alpha`的集合；
    (3)已知角`alpha`是第二象限角，试确定`2alpha`、`alpha/2`所在的象限；
    (4)若`theta`角的终边与`168°`角的终边相同，求在`[0°，360°)`内终边与`theta/3`角的终边相同的角．

提示	示范
(提示内容)
解:(1)集合为`{alpha|alpha=2kpi+pi/2，k∈ZZ}∪{alpha|alpha=2kpi+(3pi)/2，k∈ZZ}={alpha|alpha=kpi+pi/2，k∈ZZ}`   (2)由于`y=-|x|`的图象是三、四象限的平分线，故在`0°～360°`问所对应的两个角分别为225°及315°，从而角`alpha`的集合为`S={alphalalpha=k•360°+225°或alpha=k•360°+315°，k∈ZZ}`     (3)∵`alpha`是第二象限角，     ∴`k•360°+90°<alpha<k•360°+180°，k∈ZZ`     ∴`2k•360°+180°<alpha<2k•360°+360°，k∈ZZ`     ∴`2alpha`是第三、四象限角或角的终边在`y`轴负半轴上     ∵`k•180°+45°<alpha/2<k•180°+90°，k∈ZZ`，     当`k=2m(m∈ZZ)`时，`m•360°+45°<alpha/2<m•360°+90°`     当`k=2m+1(m∈ZZ)`时，`m•360°+225°<alpha/2<m•360°+270°`     ∴`alpha/2`为第一或第三象限角     (4)`theta=k•360°+168°，k∈ZZ，theta/3=k•120°+56°，k∈ZZ`     依题意得`0≤k•120°+56°<360°`，当`k=0，1，2`时，`k•120°+56°在[0°，360°)`内，     ∴`theta/3=56°，176°，296°`．     评注:(1)求终边相同的角的集合，方法是先求出`[0，2pi)`之间符合条件的角，再根据周期性写出符合条件的角的集合；(2)在解题过程中注重利用图形增强直观性．

    2、已知角`alpha`的终边在直线`y=-3x`上，求`10sinalpha+3secalpha`的值.

提示	示范
(提示内容)
解:设`alpha`终边上任一点为`P(k，-3k)`，则`r=root()(x^2+y^2)=root()(k^2+(-3k)^2)=root()(10)|k|`．     当`k>0`时,`r=root()(10)|k|`,     ∴`sinalpha=(-3k)/(root()(10)|k|)=-3/(root()(10))，secalpha=(root()(10)k)/k=root()(10)`     ∴`10sinalpha+3secalpha=-3root()(10)+3root()(10)=10`.     当`k<0`时,`r=-root()(10)|k|`,     ∴`sinalpha=(-3k)/(-root()(10)|k|)=3/(root()(10)),secalpha=(-root()(10)k)/k=-root()(10)`     ∴`10sinalpha+3secalpha=3root()(10)-3root()(10)=10`.   评注:(1)角的终边在直线`y=-3x`上，在直线上任取一点`P(k，-3k)`，要清楚当`k>0`时，`P(k，-3k)`是第四象限的点，角`alpha`的终边在第四象限；当`k<0`时，`P(k，-3k)`是第二象限的点，角`alpha`的终边在第二象限．这与角`alpha`的终边在`y=-3x`上是一致的．做此类问题时一定注意分类讨论．   (2)熟记几组常用的勾股数组，如`(3，4，5)`，`(5，12，13)`，`(7，24，25)`，`(8，15，17)`，`(9，40，41)`等会给我们的解题带来很多方便．   (3)若角`alpha`已经给定，不论点`P`选择在`alpha`的终边上的什么位置，角`alpha`的三角函数值都是确定的；另一方面，如果角`alpha`终边上一点坐标已经确定，那么根据三角函数定义，角`alpha`的三角函数值也都是确定的．