|
一、复习目标 1、了解正弦、余弦、正切函数图象,会用“五点法”画正弦、余弦函数和函数`y=Asin(omegax+varphi)`的简图,理解`A`,`omega`,`varphi`的物理意义; 2、理解周期函数与最小正周期的意义; 3、理解正弦函数、余弦函数、正切函数的性质; 4、会用已知三角函数值求角,并会用符号`arcsinx、arc cosx、arctanx`表示. 二、重点难点 难点:三角函数图象与性质的综合应用. 三、特别提示 |
| 知识梳理 1、正弦曲线`y=sinx`的变换
|
|
应用举例
二、案例示范
1、已知函数`f(x)=sin^2x+root()(3)sinxcosx+2cos^2x`,`x in R`.
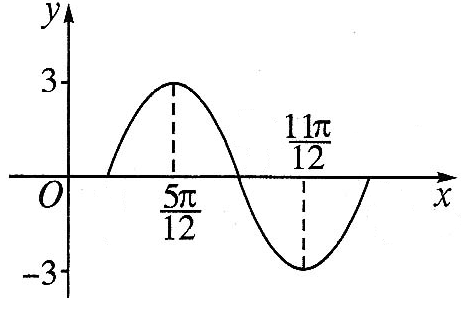
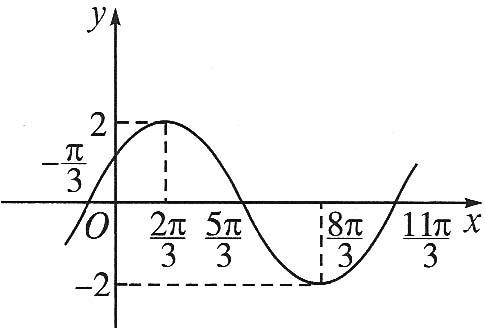
2、如图,函数`y=Asin(omegax+varphi)(A>0,omega>0)`的图象上相邻的最高点与最低点的坐标分别为`((5pi)/12,3)`和`((11pi)/12,-3)`,求该函数的解析式.
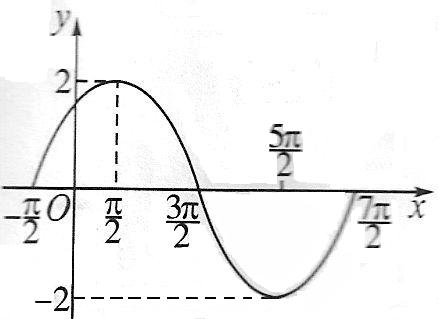
3、已知函数`f(x)=sin(omegax+varphi)(omega>O,0≤omega≤pi)`是R上的偶函数,其图象关于点`M((3pi)/4,0)`对称,且在区间`[0,pi/2]`上是单调函数,求`varphi`和`omega`的值.
|
|
实践体验 1、用五点作图法画出函数`y=root()(3)sin(x/2)+cos(x/2)`的图象,并说明这个图象是由`y=sinx`的图象经过怎样的变换得到
2、如图,`y=Asin(omegax+varphi)`图象的一段,求其解析式. 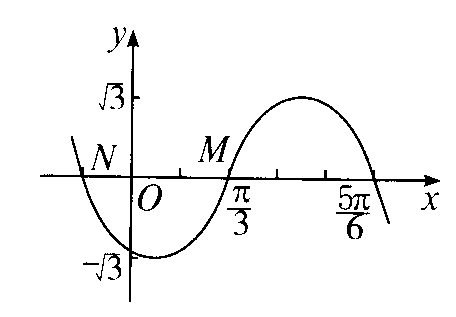
|
| 拓展探究 已知函数`f(x)=(6cos^4x+5sin^2x-4)/(cos2x)`,求`f(x)`的定义域,判断它的奇偶性,并求其值域.
|
|
|
|
|
学习感悟 |