二、重点难点
    重点:同角的三角函数的基本关系式, 正弦、余弦的诱导公式.

    难点:同角的三角函数的基本关系式, 正弦、余弦的诱导公式的综合应用.

    三、特别提示
  1、利用同角三角函数的基本关系式时要细心观察题目的特征，注意公式的合理选用，特别要注意开方时的符号选取，切割化弦是常用的方法．
  2、学会利用方程的思想解三角题，对于`sinalpha+cosalpha`，`sinalpha*cosalpha`，`sinalpha-cosalpha`三个式子，已知其中一个式子的值，可求其余两个式子的值．
  3、同角三角函数的基本关系反映了同一角的不同三角函数间的必然联系，诱导公式则揭示了不同象限的三角函数的内在规律．我们已经看到，它们对三角函数式的求值、化简、证明等具有重要作用，需要熟练掌握，灵活应用．
  4、在已知一个角的一个三角函数值，求这个角的其他三个函数值时，要注意题设中的角的范围，需要时并就不同象限分别求出相应的值．
    5、在利用同角三角函数的基本关系化简、求值时，要注意用“是否是同角”来区分和选用公式．
  6、在应用诱导公式进行三角式的化简、求值时，应注意公式中符号的选取及函数名称的正确判断．同时必须对一些特殊角的三角函数值熟记，做到“见角知值，见值知角”．

   

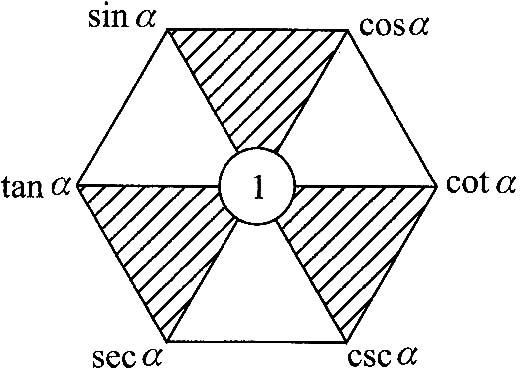
    (1)三条对角线上两函数的积等于1；(2)任一顶点的函数等于和它相邻的两顶点上的函数的乘积；(3)三个倒立的三角形肩上两数的平方和等于下面顶点上函数的平方．
    二、诱导公式
  1、`2kpi+alpha(k∈ZZ)`，`-alpha`，`pi+-alpha`，`2pi-alpha`的三角函数等于`alpha`______的三角函数值，前面加上一个把`alpha`看成______角时原函数值所在象限的符号．
    简记：函数名称同，符号看象限．
  2、`pi/2+-alpha`，`(3pi)/2+-alpha`三角函数值等于`alpha`的_______函数值，前面加上一个把`alpha`看成_____角时原函数值所在象限的符号．
    记忆方法为：函数名互余，符号看象限．
    统一记为：奇变偶不变，符号看象限．(注：奇、偶指`pi/2`的奇数倍或偶数倍)
　

    应用举例
    一、应用特点
    1、运用同角三角函数基本关系求值和化简
    2、三角函数的化简、证明
    3、用诱导公式解题

    二、案例示范
    (回味相关知识与方法，寻找解题办法，若有困难，可以参考“提示”，还有困难，可以参考“解答”或倾听老师的分析示范)

    1、已知`alpha`是第一象限的角，且`cosalpha=5/13`，求`sin(alpha+pi/4)/cos(2alpha+4pi)`的值.

提示	示范
利用两角和与差的三角函数公式和诱导公式将所求式子展开.
解:∵`alpha`是第一象限的角，`cosalpha=5/13`．     ∴`sinalpha=12/13`     ∴`sin(alpha+pi/4)/cos(2alpha+4pi)`= `(root()(2)/2(sinalpha+cosalpha))/cos(2alpha)`     = `(root()(2)/2(sinalpha+cosalpha))/(cos^2alpha-sin^2alpha)`= `(root()(2)/2)/(cosalpha-sinalpha)`     = `(root()(2)/2)/(5/13-12/13)`     = `-(13root()(2))/14`     评注:在求解过程中，要注意三角函数符号的选择，这在本章知识中是很重要的．

提示	示范
对于诸如`-alpha，pi+-alpha，pi/2，pi/2+-alpha，(3pi)/2+-alpha，2pi+-alpha，2kpi+-alpha`等诱导公式可利用“奇变偶不变，符号看象限”来处理
解:(1)`f(alpha)=(sinalpha*cosalpha*cotalpha)/((-cotalpha)sinalpha)=-cosalpha`     (2)∵`cos(alpha-(3pi)/2)=-sinalpha`     ∴`sinalpha=-1/5，cosalpha=-root()(5^2-1)/5=-2/5root()(6)`     ∴`f(alpha)=2/5root()(6)`     (3)∵`-1860°=-6xx360°+300°`     ∴`f(-1860°)=-cos(-1860°)=-cos(-6xx360°+300°)=-cos60°=-1/2`     评注:在有关三角函数的求值及诱导公式的运用中，应注意正负号的选择与变化．

    实践体验
    (在实践中提高能力，在体验中反思感悟，力求独立，力求提高)

    1、(1)化简`sin(alpha-pi/4)+cos(alpha+pi/4)`；
    (2)已知`pi<alpha<2pi`，`cos(alpha-9pi)=-3/5`，求`cos(alpha-(11pi)/2)`的值.

提示	示范
(提示内容)
解:(1)原式`sin(alpha-pi/4)+cos[pi/2+(alpha-pi/4)]=sin(alpha-pi/4)-sin(alpha-pi/4)=0`     (2)`cos(alpha-9pi)=cos(alpha-pi)=-3/5`     ∴`cosalpha=3/5`     ∵`pi<alpha<2pi`     ∴`sinalpha=-4/5`     `tanalpha=sinalpha/cosalpha=-4/3`     ∴`cot(alpha-(11pi)/2)=-cot((3pi)/2-alpha)=-tanalpha=4/3`     评注:(1)在利用诱导公式进行化简时，要有整体思维意识，即利用“换元”的思想．     (2)应用诱导公式时，要准确地判断“函数名称”及“正负号”，一般可用“奇变偶不变，符号看象限”这个口诀来确定.

    2、(1)若`tanalpha=root()(2)`，求值：
    ①`(cosalpha+sinalpha)/(cosalpha-sinalpha)`；
    ②`2sin^2alpha-sinalphacosalpha+cos^2alpha`．
    (2)求值：`(1-sin^6x-cos^6x)/(1-sin^4x-cos^4x)`.

提示	示范
(提示内容)
解:(1)①原式=`(1+sinalpha/cosalpha)/(1-sinalpha/cosalpha)=(1+root()(2))/(1-root()(2))=-3-2root()(2)`     ②∵`cos^2alpha=1/(1+tan^2alpha)=1/3`     ∴原式=`cos^2alpha(2tan^2alpha-tanalpha+1)=(5-root()(2)/3)`     (2)∵`sin^6x+cos^6x=(sin^2x+cos^2x)(sin^4x-sin^2x*cos^2x+cos^4x)=(sin^2x+cos^2x)^2-3sin^2x*cos^2x`=`1-3sin^2x*cos^2x`      又∵`sin^4x+cos^4x=(sin^2x+cos^2x)^2-2sin^2x*cos^2x=1-2sin^2x*cos^2x`     ∴原式=`(1-sin^6x-cos^6x)/(1-sin^4x-cos^4x)=3/2`     评注:(1)问题的处理充分利用了平方关系：`sin^2x+cos^2x=1`，进行了整体转化．   (2)在三角函数式的求值中，若已知`sinx+cosx`，`sinx-cosx`，`sinx*cosx`，`tanx`中的一个式子的值，可求出其余三个式子的值，继而解决有关的问题．该问题的难点在于开方时符号的选取，解题时要注意角的范围的挖掘．   (3)这是一组在已知`tanalpha=m`的条件下，求关于`sinalpha、cosalpha`的齐次式的问题，解这类问题需注意以下两点：   ①一定是关于`sinalpha、cosalpha`的齐次式(或能化为齐次式)的三角函数式；   ②∵`cosalpha≠O`，可用`cos^nalpha(n∈N^*)`除之，这样可以将被求 式化为关于`tanalpha`的表示式，可整体代入`tanalpha=m`的值，从而完 成被求式的求值．

    学习感悟
  1、运用诱导公式的重点在于函数名称与符号的正确判断和使用，在运用同角关系的平方关系时，关键在于讨论角的范围．应用同角三角函数关系式的顺序是：先平方，后倒商．如已知`sinalpha=1/3`，`alpha`为第二象限角，求`tanalpha`时，先算`cosalpha`，再计算`tanalpha`．
  2、在进行三角函数化简和三角恒等式证明时，一般思路是将切化弦，但在某些特殊问题中就不要化切为弦，只须利用倒数关系即可，否则解法较繁，如“求证`(tanalpha-cotbeta)/(tanbeta-cotalpha)=tanalpha*cotbeta`”，利用倒数关系可得简证．
    3、利用诱导公式把任意三角函数化为锐角的三角函数的步骤是：
    任意角的三角函数`->`正角的三角函数`->``0°～360°`角的三角函数`->`锐角的三角函数．
    即“去负——脱周——化锐”