§4.3 两角和与差的三角函数

第四章三角函数
§4.3 两角和与差的三角函数

复习目标

知识梳理

应用举例

实践体验

拓展探究

基础训练

提高训练

学习感悟

一、复习目标
掌握两角和与差的正弦、余弦、正切公式．

二、重点难点
重点:两角和与差的正弦、余弦、正切公式及其应用.

难点:两角和与差的正弦、余弦、正切公式及其灵活应用.

    三、特别提示
    1、公式成立的条件：在三角公式中，只有当公式的等号两端都有意义时，公式才成立．
    2、记忆公式时，要明确角、函数和排列顺序，以及连接符号“+”“-”的变化特点．
3、公式应用要讲究一个“活”字，即正用、逆用、变形用，还要创造条件用公式，如拆角、配角技巧： $β$ $= (α + β) - α$ ， $2 α = (α + β) + (α - β)$ 等．
4、当角 $α$ 、 $β$ 中有一个角为 $90 °$ 的整数倍时，使用诱导公式较为简便，诱导公式是两角和与差的三角函数公式的特例．
5、辅助角法是三角变换的重要技巧，应用如下重要结论： $a sin x + b cos x = \sqrt[]{a^{2} + b^{2}} sin (x + ϕ)$ 解题，历届高考中频频出现，应予以重视．

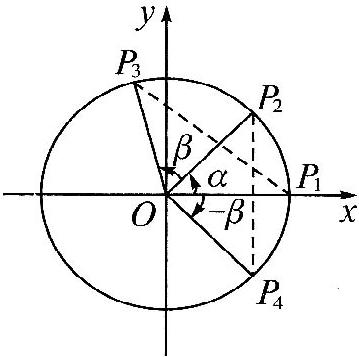
知识梳理
1、在两角和与差的公式中，以公式

C_{α + β}

为最基本，其推导过程应熟练掌握．

如图，点

P_{1} 、 P_{2} 、 P_{3} 、 P_{4}

的坐标分别为

P_{1} (1 ， 0)

、

P_{2} (cos α ， sin α)

、

P_{3} (cos (α + β) ， sin (α + β))

、

P_{4} (cos (- β) ， sin (- β))

由

P_{1} P_{3} = P_{2} P_{4}

及两点间距离公式得

2 - 2 cos (α + β) = 2 - 2 (cos α cos β - sin α sin β)

，

整理得

cos (α + β) = cos α cos β - sin α sin β [C_{α + β}]

，本公式中

α 、 β

对任意的角都成立．

2、① $cos (α + β) = cos α cos β - sin α sin β [C_{α + β}] \overset{以 - β 代 β}{\to}$ $cos (α - β) = cos α cos β + sin α sin β [C_{α - β}]$

$\overset{由诱导公式}{\to}$ $sin (α + β) = sin α cos β + cos α sin β [S_{α + β}] \overset{以 - β 代 β}{\to} sin (α - β) = sin α cos β - cos α sin β [S_{α - β}]$

② $\frac{S_{α + β}}{C_{α + β}}$ 可得 $tan (α + β) = \frac{tan α + tan β}{1 - tan α tan β} [T_{α + β}]$ ， $\frac{S_{α - β}}{C_{α - β}}$ 可得 $tan (α - β) = \frac{tan α - tan β}{1 + tan α tan β} [T_{α - β}]$

3、 $a sin α + b cos α = \sqrt[]{a^{2} + b^{2}} sin (α + ϕ)$ ，其中 $cos ϕ = \frac{a}{\sqrt{a^{2} + b^{2}}}$ ， $sin ϕ = \frac{b}{\sqrt{a^{2} + b^{2}}}$ ， $tan ϕ = \frac{b}{a}$ ．
$ϕ$ 的终边所在象限由________来确定．

    应用举例
    一、应用特点
    1、两角和与差的三角函数公式的应用
    2、公式的逆用、拆变角等技巧
    3、和差角公式与方程、函数相结合题型

二、案例示范
(回味相关知识与方法，寻找解题办法，若有困难，可以参考“提示”，还有困难，可以参考“解答”或倾听老师的分析示范)

1、化简： $2 sin l 30 ° + sin 100 ° (1 + \sqrt[]{3} tan 370 °)$

提示	示范
切化弦，利用和差角公式
解:原式= $2 sin 50 ° + sin 80 ° (1 + \sqrt[]{3} tan 370 °)$ = $2 cos 40 ° + cos 10 ° \cdot \frac{cos 10 ° + \sqrt[]{3} sin 10 °}{cos 10 °}$ = $2 cos 40 ° + 2 (\frac{1}{2} cos 10 ° + \frac{\sqrt[]{3}}{2} sin 10 °)$ = $2 cos 40 ° + 2 sin 40 °$ = $2 \sqrt[]{2} sin 85 °$ 评注:本题通过对公式的灵活运用，如“切化弦”“引入辅助角”恰当地运用和角公式，为解题寻求合理简捷的运算途径．一般地，对 $a sin α + b cos α$ ，当 $\frac{\| a \|}{\| b \|} = \sqrt[]{3}$ ，1， $\frac{1}{\sqrt[]{3}}$ 时可利用特殊值引入辅助角，再通过和角公式逆用，可对其化简，如： $sin α + \sqrt[]{3} cos α = 2 sin (α + 60 °) ， sin α + cos α = \sqrt[]{2} sin (α + 45 °)$ 等.

2、已知

\frac{π}{2} < β < α < \frac{3 π}{4}

，

cos (α - β) = \frac{12}{13}

，

sin (α + β) = - \frac{3}{5}

，求

sin 2 α

和

cos 2 β

的值.

提示	示范
由 $2 α = (α + β) + (α - β)$ ， $2 β = (α + β) - (α - β)$ 可进行角的拆换
解:∵ $\frac{π}{2} < β < α < \frac{3 π}{4}$ ∴ $0 < α - β < \frac{π}{4} ， π < α + β < \frac{3 π}{2}$ ∴ $sin (α - β) = \frac{5}{13} ， cos (α + β) = - \frac{4}{5}$ ∴ $sin 2 α = sin (α + β) + (α - β)$ = $sin (α + β) cos (α - β) + cos (α + β) sin (α - β)$ = $- \frac{3}{5} \times \frac{12}{13} + (- \frac{4}{5}) \times \frac{5}{13}$ = $- \frac{56}{65}$ $cos 2 β = cos [(α + β) - (α - β)]$ = $cos (α + β) cos (α - β) + sin (α + β) sin (α - β)$ = $- \frac{63}{65}$ 评注:本题解题的关键是处理好角与角之间的关系：由 $2 α = (α + β) + (α - β)$ ， $2 β = (α + β) - (α - β)$ ．通常情况下对有关求值与证明问题求解时，先分析条件与结论中角之间的关系，达到角的统一，从而得到有效的解题方法．

3、

tan α 、 tan β

是方程

x^{2} - 3 x - 3 = 0

的两根，求

{sin}^{2} (α + β) - 3 sin (α + β) cos (α + β) - 3 {cos}^{2} (α + β)

的值.

提示	示范
弦化切，两角和的正切并结合韦达定理．
解:由题意得 ${\begin{cases} tan α + tan β = 3 \\ tan α tan β = - 3 \end{cases}$ $\Rightarrow$ $tan (α + β) = \frac{tan α + tan β}{1 - tan α tan β} = \frac{3}{4}$ ∴ ${sin}^{2} (α + β) - 3 sin (α + β) cos (α + β) - 3 {cos}^{2} (α + β)$ = $\frac{{sin}^{2} (α + β) - 3 sin (α + β) cos (α + β) - 3 {cos}^{2} (α + β)}{{sin}^{2} (α + β) + {cos}^{2} (α + β)}$ = $\frac{{tan}^{2} (α + β) - 3 tan (α + β) - 3}{{tan}^{2} (α + β) + 1}$ = $- 3$ 评注:此题解题的关键是利用根与系数关系求得 $tan (α + β)$ ．解这类问题主要是应坚持三角运算的基本原则．注意公式的灵活运用及角的配凑变换；还要紧抓已知条件，灵活使用已知条件，深刻地挖掘已知条件．

实践体验
(在实践中提高能力，在体验中反思感悟，力求独立，力求提高)

    1、不查表求下列各式的值：
    (1) $sin (x + 60 °) + 2 sin (x - 60 °) - \sqrt[]{3} cos (120 ° - x)$
    (2) $\frac{2 sin 80 ° - cos 70 °}{cos 20 °}$

    提示示范　

    (提示内容)

    解:(1)原式= $sin x cos 60 ° + cos x sin 60 ° + 2 (sin x cos 60 ° - cos x sin 60 °) - \sqrt[]{3} (cos 120 ° cos 3 x + sin 120 ° sin x)$
    = $\frac{3}{2} sin x - \frac{\sqrt[]{3}}{2} cos x + \frac{\sqrt[]{3}}{2} cos x - \frac{3}{2} sin x$
    = $0$
    (2)原式= $\frac{2 sin (60 ° + 20 °) - cos (90 ° - 20 °)}{cos 20 °}$
    = $\frac{\sqrt[]{3} cos 20 ° + sin 20 ° - sin 20 °}{cos 20 °}$
    = $\sqrt[]{3}$
   评注:本题属“给角求值型”题，后面我们将详细论述．这类问题求解的基本策略是：化异角为同角，用已知角表示未知角，从众多角中选取一个作基本角，其他角用基本角表示出来，在求解过程中尽量使式子中出现特殊角．这是处理三角问题的基本思路

    2、(1)已知 $cos (\frac{π}{4} - α) = \frac{3}{5}$ ， $sin (\frac{3 π}{4} + β) = \frac{5}{13}$ ，其中 $\frac{π}{4} < α < \frac{3 π}{4}, 0 < β < \frac{π}{4}$ ，求 $sin (α + β)$ 的值
    (2)已知 $α 、 β$ 是锐角，且 $sin α = \frac{\sqrt[]{5}}{5} ， sin β = \frac{\sqrt[]{10}}{10}$ ，求 $α + β$

    提示示范　

    (提示内容)

    解:(1)∵ $\frac{π}{4} < α < \frac{3 π}{4} ， 0 < β < \frac{π}{4}$
    $∴ - \frac{π}{2} < \frac{π}{4} - α < 0 ， \frac{3 π}{4} < \frac{3 π}{4} + β < π$
    $∴ sin (\frac{π}{4} - α) = - \sqrt[]{1 - {cos}^{2} (\frac{π}{4} - α)} = - \sqrt[]{1 - {(\frac{3}{5})}^{2}} = - \frac{4}{5}$
    $cos (\frac{3 π}{4} + β) - \sqrt[]{1 - {sin}^{2} (\frac{3 π}{4} + β)} = - \sqrt[]{1 - {(\frac{5}{13})}^{2}} = - \frac{12}{13}$
     $cos [\frac{π}{2} + (α + β)] = cos [(\frac{3 π}{4} + β) - (\frac{π}{4} - α)]$
     $= cos (\frac{3 π}{4} + β) cos (\frac{π}{4} - α) + sin (\frac{3 π}{4} + β) sin (\frac{π}{4} - α)$
     $= (- \frac{12}{13}) \times \frac{3}{5} + \frac{5}{13} \times (- \frac{4}{5}) = - \frac{56}{65}$
    ∴ $sin (α + β) = - cos [\frac{π}{2} + (α + β)] = \frac{56}{65}$
    (2)∵ $0 < α < \frac{π}{2} ， 0 < β < \frac{π}{2}$
    ∴ $0 < α + β < π$
    又∵ $cos α = \frac{2 \sqrt[]{5}}{5} ， cos β = \frac{3 \sqrt[]{10}}{10}$
    ∴ $cos (α + β)$ = $cos α cos β - sin α sin β$
     $= \frac{2 \sqrt[]{5}}{5} \times \frac{3 \sqrt[]{10}}{10} - \frac{\sqrt[]{5}}{5} \times \frac{\sqrt[]{10}}{10}$
     $= \frac{\sqrt[]{2}}{2}$
    又∵在 $0 ～ π$ 之间，余弦值为 $\frac{\sqrt[]{2}}{2}$ 的角度只有 $\frac{π}{4}$
     $∴ α + β = \frac{π}{4}$
    评注:(1)是给值求值问题，解这类问题应认真分析已知式中角与未知式中角的关系，再决定如何利用已知条件，采用哪些公式，避免盲目处理相关角的三角函数式，以免造成不必要的麻烦，要整体地把握公式，认真考虑角的整体运用，这往往要用到常见的角的变换，如 $α = (α + β) - α ， 2 α = (α + β) + (α - β) ， α + \frac{π}{4} = (α + β) - (β - \frac{π}{4})$ 等.

拓展探究
(1)化简

\frac{\sqrt[]{2}}{4} sin (\frac{π}{4} - x) + \frac{\sqrt[]{6}}{4} cos (\frac{π}{4} - x)

；

(2)已知

tan (α + β) = 2 tan β

，求证：

3 sin α = sin (α + 2 β)

提示	示范
(提示内容)
解:(1) $\frac{\sqrt[]{2}}{4} sin (\frac{π}{4} - x) + \frac{\sqrt[]{6}}{4} cos (\frac{π}{4} - x)$ = $\frac{\sqrt[]{2}}{2} (\frac{1}{2} sin (\frac{π}{4} - x) + \frac{\sqrt[]{6}}{2} cos (\frac{π}{4} - x))$ = $\frac{\sqrt[]{2}}{2} (cos (\frac{π}{3}) sin (\frac{π}{4} - x) + sin (\frac{π}{3}) cos (\frac{π}{4} - x))$ = $\frac{\sqrt[]{2}}{2} sin (\frac{π}{4} - x + \frac{π}{3})$ = $\frac{\sqrt[]{2}}{2} sin (\frac{7 π}{12} - x)$ (2)由已知 $tan (α + β) = 2 tan β$ ，可得 $\frac{sin (α + β)}{cos (α + β)} = \frac{2 sin β}{cos β}$ ∴ $sin (α + β) \cdot cos β = 2 cos (α + β) \cdot sin β$ 而 $sin (α + 2 β) = sin [(α + β) + β]$ = $sin (α + β) \cdot cos β + cos (α + β) \cdot sin β$ = $2 cos (α + β) \cdot sin β + cos (α + β) \cdot sin β$ = $3 cos (α + β) \cdot sin β$ 又 $sin α = sin [(α + β) - β]$ = $sin (α + β) \cdot cos β - cos (α + β) \cdot sin β$ = $2 cos (α + β) \cdot sin β - cos (α + β) \cdot sin β$ = $cos (α + β) \cdot sin β$ 故 $sin (α + 2 β) = 3 sin α$ 评注:(1) $a sin x + b cos x = \sqrt[]{a^{2} + b^{2}} sin (x + ϕ)$ (其中 $ϕ$ 角的终边所在象限由 $a 、 b$ 的符号确定， $ϕ$ 角满足 $cos ϕ = \frac{a}{\sqrt[]{a^{2} + b^{2}}}$ , $sin ϕ = \frac{b}{\sqrt[]{a^{2} + b^{2}}}$ ，这是经常用到的一个公式，它可把含 $sin x 、 cos x$ 的一次式的三角函数式化为 $A sin (x + ϕ)$ 的形式，从而进一步探索三角函数的性质． (2)分析条件等式与论证式中角和函数名称的差异，从而进行配角，再利用同角三角函数关系式消除函数名称的差异．对于三角恒等式的证明，实质也是消除等式两边的差异，有目的地化繁为简，左右归一或变更论证．

基础训练

1、若

α 、 β \in (0 ， \frac{π}{2})

，

cos (α - \frac{β}{2}) = \frac{\sqrt[]{3}}{2}

，

sin (\frac{α}{2} - β) = - \frac{1}{2}

，则

cos (α + β)

的值等于( )
A.

- \frac{\sqrt[]{3}}{2}

- \frac{1}{2}

\frac{1}{2}

\frac{\sqrt[]{3}}{2}

2、已知

sin α = \frac{\sqrt[]{5}}{5}

，

sin β = \frac{\sqrt[]{10}}{10}

，且

α 、 β

为锐角，则

α + β

的值是(   )
    A.45°     B.135°或45°     C.135°     D.以上都不对
    3、已知

α 、 β \in (\frac{3 π}{4} ， π)

，

sin (α + β) = - \frac{3}{5}

，

sin (β - \frac{π}{4}) = \frac{12}{13}

，则

cos (α + \frac{π}{4})

等于( )
A.

\frac{13}{65}

- \frac{16}{65}

\frac{56}{65}

- \frac{56}{65}

4、在

△ A B C

中，若

tan B = \frac{cos (C - B)}{sin A + sin (C - B)}

，则这个三角形是(   )
    A.锐角三角形     B.直角三角形     C.等腰三角形     D.等腰三角形或直角三角形
    5、求值

\frac{tan 20 ° + tan 40 ° + tan 120 °}{tan 20 ° tan 40 °}

=______
6、计算

(1 + tan l °) (1 + tan 2 °) (1 + tan 3 °) \dots (1 + tan 43 °) (1 + tan 44 °)

=______
7、已知

α 、 β

为锐角，

cos α = \frac{4}{5}

，

cot (α - β) = - 3

，求

sin β

的值．
8、已知

tan (\frac{π}{4} + α) = 3

，
(1)求

tan α

的值；
(2)求

sin 2 α + cos 2 α

的值．

参考答案

1、若

α 、 β \in (0 ， \frac{π}{2})

，

cos (α - \frac{β}{2}) = \frac{\sqrt[]{3}}{2}

，

sin (\frac{α}{2} - β) = - \frac{1}{2}

，则

cos (α + β)

的值等于( B )
A.

- \frac{\sqrt[]{3}}{2}

- \frac{1}{2}

\frac{1}{2}

\frac{\sqrt[]{3}}{2}

2、已知

sin α = \frac{\sqrt[]{5}}{5}

，

sin β = \frac{\sqrt[]{10}}{10}

，且

α 、 β

为锐角，则

α + β

的值是( A )
A.45° B.135°或45° C.135° D.以上都不对
3、已知

α 、 β \in (\frac{3 π}{4} ， π)

，

sin (α + β) = - \frac{3}{5}

，

sin (β - \frac{π}{4}) = \frac{12}{13}

，则

cos (α + \frac{π}{4})

等于( D )
A.

\frac{13}{65}

- \frac{16}{65}

\frac{56}{65}

- \frac{56}{65}

4、在

△ A B C

中，若

tan B = \frac{cos (C - B)}{sin A + sin (C - B)}

，则这个三角形是( B )
A.锐角三角形 B.直角三角形 C.等腰三角形 D.等腰三角形或直角三角形
5、求值

\frac{tan 20 ° + tan 40 ° + tan 120 °}{tan 20 ° tan 40 °}

=______
答案：

- \sqrt{3}

6、计算

(1 + tan 1 °) (1 + tan 2 °) (1 + tan 3 °) \dots (1 + tan 43 °) (1 + tan 44 °)

=______
答案：

2^{22}

7、已知

α 、 β

为锐角，

cos α = \frac{4}{5}

，

cot (α - β) = - 3

，求

sin β

的值．
答案：

13 \frac{\sqrt{10}}{56}

8、已知

tan (\frac{π}{4} + α) = 3

，
(1)求

tan α

的值；
(2)求

sin 2 α + cos 2 α

的值．
答案：(1)

\frac{1}{2}

\frac{7}{5}

提高训练

1、

cos 43 ° cos 77 ° + sin 43 ° cos 167 °

的值为______．
2、

\frac{sin (α + 30 °) - sin (α - 30 °)}{cos α}

的值为______.
3、若

\frac{π}{4} < α < \frac{3 π}{4} ， 0 < β < \frac{π}{4}

，且

sin (α + \frac{π}{4}) = \frac{3}{5}

，

cos (\frac{π}{4} + β) = \frac{5}{13}

，求

sin (α + β)

的值．
4、已知

sin α - sin β = \frac{1}{2}

，

cos α - cos β = 1

，

cos (α + β)

及

cos (α - β)

的值.

参考答案

1、

cos 43 ° cos 77 ° + sin 43 ° cos 167 °

的值为______
答案：

- \frac{1}{2}

2、

\frac{sin (α + 30 °) - sin (α - 30 °)}{cos α}

的值为______
答案：

\frac{56}{65}

3、若

\frac{π}{4} < α < \frac{3 π}{4} ， 0 < β < \frac{π}{4}

，且

sin (α + \frac{π}{4}) = \frac{3}{5}

，

cos (\frac{π}{4} + β) = \frac{5}{13}

，求

sin (α + β)

的值．
答案：

1

4、已知

sin α - sin β = \frac{1}{2}

，

cos α - cos β = 1

，

cos (α + β)

及

cos (α - β)

的值.
答案：

- \frac{3}{5}

\frac{3}{8}

    学习感悟
    1、求值问题有三类：
    (1)给角求值的关键是正确地选用公式，以便把非特殊角的三角函数相约或相消，从而化为特殊角的三角函数
(2)给值求值关键是找出已知与欲求式之问的角、运算及函数的差异，一般可以适当变换已知式，求得另外函数式的值，以备应用；同时也要注意变换欲求式，便于将已知式求得的函数值代入，从而达到解题的目的．
    (3)给值求角关键是先求出该角某一三角函数式的值，其次判断该角在对应区间的单调性，从而达到解题目的．
    2、化简三角函数式的要求
    (1)能求出值的应求出值；
    (2)使三角函数种数尽量少；
    (3)使项数尽量少；
    (4)尽量使分母不含三角函数，例如： $\frac{1}{sin α} = csc α$ ；
    (5)尽量使被开方数不含三角函数．
    3、无论是证明还是化简，常用的方法有：
    (1)直接应用公式；
    (2)切割化弦，异名化同名，异角化同角；
    (3)改变运算结构，升幂、降幂、和差与积的互化、通分等．

本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。