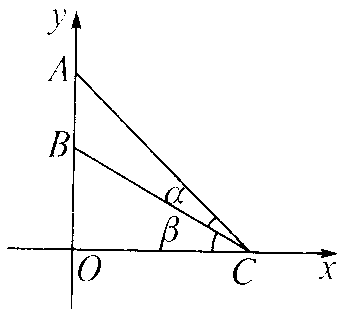§4.6 三角函数的应用

第四章三角函数
§4.6 三角函数的应用

复习目标

知识梳理

应用举例

实践体验

拓展探究

基础训练

提高训练

学习感悟

一、复习目标
掌握三角函数最值的常见求法，能运用三角函数最值解决一些实际问题．

二、重点难点
重点:三角函数最值的常见方法与实际应用.

难点:角的变换方法与角范围的讨论.

    三、特别提示
    1、要重视角的范围对三角函数最值的影响，因此要注意角的范围的讨论．
    2、三角恒等变形的实质是对角或函数名称进行转化，而转化的依据就是一系列三角公式的理解：
    ①同角三角函数关系式可实现三角函数名称的转化；
    ②诱导公式及和、差、倍角的三角函数公式可实现角与名称的转化；
    ③倍角公式还可实现三角函数式次数的转化．
    3、在进行化简时，一般变角优先，要观察三角函数式中角的特点，即有无特殊角，有无互余、互补角，角与角之间有无倍、差的关系，怎样才能实现角的统一等．同时，也要注意方程思想、消元思想的应用．

知识梳理
一、化简

化简是三角函数式求值与证明的基础，即通过一系列的恒等变形，化异为同，以达到简化运算的目的．

1、化简的标准要求

(1)能求出值的就求出值来；

(2)使三角函数式的项数、三角函数的种类及角的种类尽可能少；

(3)使三角函数式的次数尽可能低；

(4)分母中尽量不含三角函数式和根式．

2、化简的常用方法

(1)能直接使用公式时就用公式(包括正用、逆用、变形用)．

(2)常用切割化、异名化、异角化等．

3、化简的常用技巧

(1)注意特殊角的三角函数与特殊值的互化．

(2)注意利用代数上的一些恒等变形法则和分数的基本性质．

(3)对于二次根式，注意二倍角公式的逆用．

(4)注意利用角与角之间的隐含关系．

(5)注意利用“1”的恒等变形．

(6)注意条件的合理使用：

①尽可能不去破坏条件的整体结构，即要把所求式子适当变形，能使条件整体代入；

②将条件适当简化、整理或重新改造、组合，使其与所求式子更吻合．

二、求值

三角函数主要有三类求值问题

1、“给角求值”：一般所给出的角都是非特殊角，从表面来看是很难的，但仔细观察非特殊角与特殊角总有一定的关系，解题时，要利用观察得到的关系，结合三角公式转化为特殊角并且消除非特殊角的三角函数而得解．

2、“给值求值”：给出某些角的三角函数式的值，求另外一些角的三角函数值，解题关键在于“变角”，使其角相同或具有某种关系．

3、“给值求角”：实质上也转化为“给值求值”，关键也是变角，把所求角用含已知角的式子表示出来，由所得的函数值结合该函数的单调区间求得角．

三、证明
三角等式的证明可分为三角恒等式的证明与三角条件等式的证明两种．

1、证明三角恒等式的方法

证明三角恒等式的实质是消除等式两边的差异，有目的地化繁为简、左右归一或变更论证．

证明三角恒等式的常用方法为：

(1)从一边开始证得它等于另一边，可能是左边

\geq

右边，也可能是右边号左边，一般应该由繁到简；

(2)证明左、右两边都等于同一个式子(或值)．

2、证明三角条件等式的方法

首先观察条件与结论的差异，从解决某一差异人手，确定从结论开始通过变换将已知表达式代人得出结论，或通过变换已知条件得出结论，如果这两种方法都证不出来，可采用分析法；如果已知条件含参数，可采用消去参数法；

如果已知是连比的式子，可用换元法．

    应用举例
    一、应用特点
    1、三角函数的实际应用
    2、三角函数与其他知识的综合应用
    3、三角函数的创新应用

二、案例示范
(回味相关知识与方法，寻找解题办法，若有困难，可以参考“提示”，还有困难，可以参考“解答”或倾听老师的分析示范)

1、如右图，平面直角坐标系中，在 $y$ 轴的正半轴(原点除外)上给定两点 $A 、 B$ ．试在 $x$ 轴的正半轴(原点除外)上求一点 $C$ ，使么 $∠ A C B$ 取得最大值.

提示	示范
由于 $∠ A C B$ 是锐角，要求 $∠ A C B$ 的最大值，应该先研究此角的某种三角函数的最大值．为此，要先确定以 $∠ A C B$ 的某种三角函数为因变量，确定 $C$ 的位置( $C$ 的横坐标)的某个量为自变量的函数关系，此种思路有多种解法，仅写一种
解:设定点 $A$ 的坐标为 $(0 ， a)$ ， $B$ 点的坐标为 $(0 ， b)$ 且 $0 < b < a$ ，又设 $C$ 点坐标为 $(x ， 0)$ ，且 $x > 0$ ．记 $∠ A C B = α$ ， $∠ B C O = β$ ，则 $∠ A C O = α + β$ 并且 $0 < α < \frac{π}{2}$ ．如上图，有 $tan α = tan [(α + β) - β]$ = $\frac{tan (α + β) - tan β}{1 + tan (α + β) \cdot tan β}$ = $\frac{\frac{a}{x} - \frac{b}{x}}{1 + \frac{a}{x} \cdot \frac{b}{x}}$ = $\frac{a - b}{x + \frac{a b}{x}}$ ∵ $x > 0 ， 0 < b < a ，故 \frac{a b}{x} > 0$ ∴ $x + a \frac{b}{x} \geq 2 \sqrt[]{x \cdot a \frac{b}{x}} = 2 \sqrt[]{a b} > 0$ 当且仅当 $x = a \frac{b}{x}$ ，即 $x = \sqrt[]{a b}$ 时上式中等号成立．又 $a - b > 0$ ， ∴ $tan α \leq \frac{a - b}{2 \sqrt[]{a b}}$ 成立，当且仅当 $x = \sqrt[]{a b}$ 时，其中等号成立．因为 $tan α$ 在 $(0 ， \frac{π}{2})$ 内是增函数，故当 $x = \sqrt[]{a b}$ 时， $α$ 即 $∠ A C B$ 取最大值，所求 $C$ 点为 $(\sqrt[]{a b} ， 0)$ . 评注:将角应用到几何当中，用三角函数来解决几何问题，从而使几何问题代数化，这是解析几何的研究方法．

2、 (2007天津检测)定义在R上的函数

f (x)

满足

f (x) = f (x + 2)

，当

x \in [3 ， 5]

时，

f (x) = 2 - | x - 4 |

，则

f (sin 1)

，

f (cos 2)

，

f (sin (\frac{π}{6}))

的大小关系是( )
A.

f (sin (\frac{π}{6})) < f (sin 1) < f (cos 2)

f (sin 1) < f (cos 2) < f (sin (\frac{π}{6}))

f (cos 2) < f (sin 1) < f (sin (\frac{π}{6}))

f (sin 1) < f (cos 2) < f (sin (\frac{π}{6}))

提示	示范
根据函数的单调性和周期性求解．
解:设 $x \in [- 1 ， 1]$ ，则 $x + 4 \in [3 ， 5]$ ． ∵ $f (x) = f (x + 2)$ ∴ $f (x) = f (x + 4) = 2 - \| x \|$ ， $x \in [- 1 ， 1]$ ，此函数为一偶函数，且在 $[0 ， 1]$ 上为减函数 ∵ $sin l > sin (\frac{π}{6}) > sin (2 - \frac{π}{2})$ ，且 $f (sin (2 - \frac{π}{2})) = f (sin (\frac{π}{2} - 2)) = f (cos 2)$ ∴ $f (sin 1) < f (sin (\frac{π}{6})) < f (sin (2 - \frac{π}{2}))$ ，故选B 评注:(内容)

3、已知某海滨浴场的海浪高度

y

(米)是时间

t (O \leq t \leq 24 ， 单 位 ： 小 时)

的函数，记作

y = f (t)

．下表是某日各时刻的浪高数据：

经长期观测， $y = f (t)$ 的曲线可近似地看成是函数 $y = A cos ω t + b$ ．
(1)根据以上数据，求出函数 $y = A cos ω t + b$ 的最小正周期 $T$ 、振幅 $A$ 及函数表达式．
(2)依据规定，当海浪高度高于1米时才对冲浪爱好者开放．请依据(1)的结论，判断一天内的上午8:OO至晚上20:00之间，有多少时间可供冲浪者进行运动?

提示	示范
(1)由两个相等的相邻 $y$ 值对应的 $x$ 值的差求周期 $T$ ．由最大与最小 $y$ 值求振幅 $A$ ．由中间 $y$ 值点求 $b$ (2)解不等式 $A cos ω t + b > 1$ ．
解:(1)由题表中数据，知周期 $T = 12$ ∵ $ω = \frac{2 π}{T} = \frac{2 π}{12} = \frac{π}{6}$ 由 $t = 0$ ， $y = 1.5$ ，得 $A + b = 1.5$ ① 由 $t = 3$ ， $y = 1.0$ ，得 $b = 1.0$ ② ∴ $A = 0.5 ， b = 1$ ∴振幅为 $\frac{1}{2}$ ∴ $y = \frac{1}{2} cos (\frac{π}{6}) t + 1$ (2)由题知，当 $t > 1$ 时才可对冲浪者开放． ∴ $\frac{1}{2} cos (\frac{π}{6}) + 1 > 1$ ∴ $cos (\frac{π}{6}) t > 0$ ∴ $2 k π - \frac{π}{2} < \frac{π}{6} t < 2 k π + \frac{π}{2}$ 即 $12 k - 3 < t < 12 k + 3$ ③ ∵ $0 \leq t \leq 24$ ，故可令③中 $k$ 分别为0，1，2，得 $0 \leq t < 3$ 或 $9 < t < 15$ 或 $21 < t \leq 24$ ∴在规定时间上午8：00至晚上20：00之间，有6个小时时间可供冲浪者运动，即上午9:00至下午15:00 评注:(内容)

实践体验
(在实践中提高能力，在体验中反思感悟，力求独立，力求提高)

    1、化简： $\frac{1 + cos θ - sin θ}{1 - cos θ - sin θ} + \frac{1 - cos θ - sin θ}{1 + cos θ - sin θ}$ .

    提示示范　

    (提示内容)

    解:原式= $\frac{2 {cos}^{2} (\frac{θ}{2}) - 2 sin (\frac{θ}{2}) cos (\frac{θ}{2})}{2 {sin}^{2} (\frac{θ}{2}) - 2 sin (\frac{θ}{2}) cos (\frac{θ}{2})} + \frac{2 {sin}^{2} (\frac{θ}{2}) - 2 sin (\frac{θ}{2}) cos (\frac{θ}{2})}{2 {cos}^{2} (\frac{θ}{2}) - 2 sin (\frac{θ}{2}) cos (\frac{θ}{2})}$
    = $\frac{2 cos (\frac{θ}{2}) (cos (\frac{θ}{2}) - sin (\frac{θ}{2}))}{2 sin (\frac{θ}{2}) (sin (\frac{θ}{2}) - cos (\frac{θ}{2}))} + \frac{2 sin (\frac{θ}{2}) (sin (\frac{θ}{2}) - cos (\frac{θ}{2}))}{2 cos (\frac{θ}{2}) (cos (\frac{θ}{2}) - sin (\frac{θ}{2}))}$

    = $- \frac{cos (\frac{θ}{2})}{sin (\frac{θ}{2})} - \frac{sin (\frac{θ}{2})}{cos (\frac{θ}{2})}$

    = $- \frac{{cos}^{2} (\frac{θ}{2}) + {sin}^{2} (\frac{θ}{2})}{sin (\frac{θ}{2}) cos (\frac{θ}{2})}$

    = $- \frac{2}{sin θ}$

   评注:化简的原则是形式简单，三角函数名称尽量少，次数尽量低，最好不合分母，能求值的尽量求值．本题两项分子、分母都较复杂，要充分利用倍角公式进行处理．对于根式形式的三角函数式的化简常以化去根号为目标，为此常使被开方的式子配成完全平方，化简时要注意角的范围．

    2、(1)求值： $(tan 10 ° - \sqrt[]{3}) \frac{cos 10 °}{sin 50 °}$ ；
    (2)求值： $\frac{cos 15 ° sin 9 ° + sin 6 °}{sin 15 ° sin 9 ° - cos 6 °}$ ；
    (3)求值： $cot 10 ° - 4 cos 10 °$ .

    提示示范　

    (提示内容)

    解:(1) $(tan 10 ° - \sqrt[]{3}) \frac{cos 10 °}{sin 50 °}$
    = $(tan 10 ° - tan 60 °) \frac{cos 10 °}{sin 50 °}$

    = $(\frac{sin 10 °}{cos 10 °} - \frac{sin 60 °}{cos 60 °}) \frac{cos 10 °}{sin 50 °}$

    = $\frac{sin (- 50 °)}{cos 10 ° cos 60 °} \frac{cos 10 °}{sin 50 °}$

    = $- 2$

    (2)原式= $\frac{cos 15 ° sin 9 ° + sin (15 ° - 9 °)}{sin 15 ° sin 9 ° - cos (15 ° - 9 °)}$

    = $\frac{cos 15 ° sin 9 ° + sin 15 ° cos 9 ° - cos 15 ° sin 9 °}{sin 15 ° sin 9 ° - (cos 15 ° cos 9 ° + sin 15 ° sin 9 °)}$

    = $\frac{sin 15 ° cos 9 °}{- cos 15 ° cos 9 °}$

    = $- tan 15 °$

    = $- \frac{tan 45 ° - tan 30 °}{1 + tan 45 ° tan 30 °}$

    = $\sqrt[]{3} - 2$

    (3)原式= $\frac{cos 10 °}{sin 10 °} - 4 cos 10 °$

    = $\frac{cos 10 ° - 2 sin 20 °}{sin 10 °}$

    = $\frac{cos 10 ° - 2 sin (30 - 10) °}{sin 10 °}$

    = $\frac{2 cos 30 ° sin 10 °}{sin 10 °}$

    = $\sqrt[]{3}$

    评注:(1)在三角函数的恒等变形中，要始终作好“角”的文章：
    ①特殊角与特殊值的转化，[例如(1)中 $\sqrt[]{3}$ 换为 $tan 60 °$ ]；
    ②角的合并[(1)中 $10 °$ 与 $60 °$ 的合并]；
    ③角的分解[(2)中 $15 °$ 分解为 $45 ° - 30 °$ ，(3)中 $20 °$ 分解为 $30 ° - 10 °$ ]．
(2)这类求值问题是通过适当地变换，在求值的三角函数或与特殊角的三角函数或已知其值的三角函数式之间建立其联系，从而达到求值目的．

拓展探究
求证：

\frac{{cos}^{2} α}{\frac{1}{tan (\frac{α}{2})} - tan (\frac{α}{2})} = \frac{1}{4} sin 2 α

提示

示范

从函数名称上看可以先切化弦，切化弦时，可用

tan (\frac{α}{2}) = \frac{sin (\frac{α}{2})}{cos (\frac{α}{2})}

，也可用

tan (\frac{α}{2}) = \frac{sin α}{1 + cos (\frac{α}{2})}

进行．

证明:方法一：左边=

\frac{{cos}^{2} α}{\frac{cos (\frac{α}{2})}{sin (\frac{α}{2})} - \frac{sin (\frac{α}{2})}{cos (\frac{α}{2})}}

= $\frac{{cos}^{2} α}{\frac{{cos}^{2} (\frac{α}{2}) - {sin}^{2} (\frac{α}{2})}{sin (\frac{α}{2}) cos (\frac{α}{2})}}$

= $\frac{{cos}^{2} α sin (\frac{α}{2}) cos (\frac{α}{2})}{{cos}^{2} (\frac{α}{2}) - {sin}^{2} (\frac{α}{2})}$

= $\frac{{cos}^{2} α sin (\frac{α}{2}) cos (\frac{α}{2})}{cos α}$

= $sin (\frac{α}{2}) cos (\frac{α}{2}) cos α$

= $\frac{1}{2} sin α cos α$

= $\frac{1}{4} sin 2 α$

=右边

∴原式成立

方法二：左边= $\frac{{cos}^{2} α}{\frac{1 + cos (\frac{α}{2})}{sin α} - \frac{1 - cos (\frac{α}{2})}{sin α}}$

= $\frac{{cos}^{2} α sin α}{2 cos α}$

= $\frac{1}{2} sin α cos α$

= $\frac{1}{4} sin 2 α$

=右边

∴原式成立

方法三：左边= $\frac{{cos}^{2} α tan (\frac{α}{2})}{1 - {tan}^{2} (\frac{α}{2})}$

= $\frac{1}{2} {cos}^{2} α \cdot \frac{2 tan (\frac{α}{2})}{1 - {tan}^{2} (\frac{α}{2})}$

= $\frac{1}{2} {cos}^{2} α \cdot tan α$

= $\frac{1}{2} cos α sin α$

= $\frac{1}{4} sin 2 α$

=右边

∴原式成立．

评注:证明三角恒等式的实质是消除等式两边的差异，有目的地化繁为简、左右归一或变更论证．对恒等式的证明，应遵循化繁为简的原则，从左边推到右边或从右边推到左边，也可以用左右归一，变更论证等方法．常用定义法、化弦法、化切法、拆项拆角法、“1”的代换法、公式变形法，要熟练掌握基本公式，善于从中选择巧妙简捷的方法．
证明条件三角恒等式，首先应观察条件与结论之间的差异(三角函数名及结构)，从解决某一差异入手，采用条件转化法或条件代入法．条件转化法就是从已知条件出发，经过恰当的变换，推出被证式；条件代入法就是从已知条件出发，求出被证式中的某一个式子，然后代入被证式，化简证明．

基础训练

    1、在 $△ A B C$ 中，若 $l g a = l g c = l g sin B = - l g \sqrt[]{2}$ ，且 $∠ B$ 为锐角，则 $∠ A$ 是(   )
    A. $30 °$      B. $45 °$      C. $67.5 °$      D. $90 °$
    2、如果函数 $y = sin 2 x + a cos 2 x$ 的图象关于直线 $x = - \frac{π}{8}$ 对称，那么 $a$ 等于(   )
    A. $\sqrt[]{2}$       B. $- \sqrt[]{2}$     C. $1$         D. $- 1$
    3、设 $α 、 β \in (- \frac{π}{2} ， \frac{π}{2})$ ，那么 $α < β$ 是 $tan α < tan β$ 的(   )
    A.充分而不必要条件     B.必要而不充分条件     C.充分必要条件     D.既不充分也不必要条件
    4、如下图所示，有一广告气球，直径为 $6 c m$ ，放在公司大楼上空，当行人仰望气球中心的仰角 $∠ B A C = 30 °$ 时，测得气球的视角为 $β = 1 °$ ，若 $θ$ 很小时，可取 $sin θ \approx θ$ ，试估算该气球的高 $B C$ 的值约为(   )

    A. $70 m$      B. $86 m$      C. $102 m$      D. $118 m$
    5、已知 $a \in R$ ，函数 $f (x) = sin x - | a |$ ， $x$ $\in R$ 为奇函数，则 $a$ 等于( )
    A. $0$      B. $1$      C. $- 1$      D. $\pm 1$
    6、函数 $y = l g (cos 2 x)$ 的单调增区间为______
    7、函数 $f (x) = sin x cos x$ 的最小正周期是______
    8、在 $△ A B C$ 中,角 $A 、 B 、 C$ 的对边分别为 $a 、 b 、 c$ ， $2 {sin}^{2} C = 3 cos C$ ， $c = \sqrt[]{7}$ ，又 $△ A B C$ 的面积为 $\frac{3 \sqrt[]{3}}{2}$ ．
    求：(1)角 $C$ 的大小；
    (2) $a + b$ 的值．

参考答案

1、在

△ A B C

中，若

l g a = l g c = l g sin B = - l g \sqrt[]{2}

，且

∠ B

为锐角，则

∠ A

是( C )
A.

30 °

45 °

67.5 °

90 °

2、如果函数

y = sin 2 x + a cos 2 x

的图象关于直线

x = - \frac{π}{8}

对称，那么

a

等于( D )
A.

\sqrt[]{2}

- \sqrt[]{2}

1

- 1

3、设

α 、 β \in (- \frac{π}{2} ， \frac{π}{2})

，那么

α < β

是

tan α < tan β

的( C )
A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件
4、如下图所示，有一广告气球，直径为

6 c m

，放在公司大楼上空，当行人仰望气球中心的仰角

∠ B A C = 30 °

时，测得气球的视角为

β = 1 °

，若

θ

很小时，可取

sin θ \approx θ

，试估算该气球的高

B C

的值约为( B )

70 m

86 m

102 m

118 m

5、已知

a \in R

，函数

f (x) = sin x - | a |

，

x

\in R

为奇函数，则

a

等于( A )
A.

0

1

- 1

\pm 1

6、函数

y = l g (cos 2 x)

的单调增区间为______
答案：

(k π - \frac{π}{4} ， k π] (k \in ℤ)

7、函数

f (x) = sin x cos x

的最小正周期是______
答案：

π

8、在

△ A B C

中,角

A 、 B 、 C

的对边分别为

a 、 b 、 c

，

2 {sin}^{2} C = 3 cos C

，

c = \sqrt[]{7}

，又

△ A B C

的面积为

\frac{3 \sqrt[]{3}}{2}

．
求：(1)角

C

的大小；
(2)

a + b

的值．
答案：(1)

60 °

(2)

5

提高训练

1、

cos α = - \frac{\sqrt[]{3}}{2}

”是“

α = 2 k π + \frac{5 π}{6} ， k \in z

”的(   )
    A.必要不充分条件     B.充分不必要条件     C.充分必要条件     D.既不充分又不必要条件
    2、若

f (sin x) = 3 - cos 2 x

，则

f (cos x)

等于( )
A.

3 - cos 2 x

3 - sin 2 x

3 + cos 2 x

3 + sin 2 x

3、如右图，函数

y = 2 sin (π x + ϕ)

，

x \in ℝ

(其中

0 \leq ϕ \leq \frac{π}{2}

)的图象与

y

轴交于点

(0 ， 1)

(1)求

ϕ

的值；
(2)设

P

是图象上的最高点，

M 、 N

是图象与

z

轴的交点，求

P M

与

P N

的夹角．

    4、已知水渠在过水断面面积为定值的情况下，过水湿周越小，其流量越大，现有以下两种设计(如下图)，
    下图①的过水断面为等腰 $△ A B C$ ， $A B = B C$ ，过水湿周 $l_{1} = A B + B C$ ．
    下图②的过水断面为等腰梯形 $A B C D ， A B = C D ， A D ∥ B C ， ∠ B A D = 60 °$ ，过水湿周 $l_{2} = A B + B C + C D$ ．

    若 $△ A B C$ 与梯形 $A B C D$ 的面积都为 $S$ ，
(1)分别求 $l_{1}$ 和 $l_{2}$ 的最小值；
    (2)为使流量最大，给出最佳设计方案．

参考答案

1、

cos α = - \frac{\sqrt[]{3}}{2}

”是“

α = 2 k π + \frac{5 π}{6} ， k \in ℤ

”的( A )
A.必要不充分条件 B.充分不必要条件 C.充分必要条件 D.既不充分又不必要条件
2、若

f (sin x) = 3 - cos 2 x

，则

f (cos x)

等于( C )
A.

3 - cos 2 x

3 - sin 2 x

3 + cos 2 x

3 + sin 2 x

3、如右图，函数

y = 2 sin (π x + ϕ)

，

x \in ℝ

(其中

0 \leq ϕ \leq \frac{π}{2}

)的图象与

y

轴交于点

(0 ， 1)

(1)求

ϕ

的值；
(2)设

P

是图象上的最高点，

M 、 N

是图象与

z

轴的交点，求

P M

与

P N

的夹角．

    答案：(1) $\frac{π}{6}$ (2) $a r cos (\frac{15}{17})$
    4、已知水渠在过水断面面积为定值的情况下，过水湿周越小，其流量越大，现有以下两种设计(如下图)，
    下图①的过水断面为等腰 $△ A B C$ ， $A B = B C$ ，过水湿周 $l_{1} = A B + B C$ ．
    下图②的过水断面为等腰梯形 $A B C D ， A B = C D ， A D ∥ B C ， ∠ B A D = 60 °$ ，过水湿周 $l_{2} = A B + B C + C D$ ．

    若 $△ A B C$ 与梯形 $A B C D$ 的面积都为 $S$ ，
(1)分别求 $l_{1}$ 和 $l_{2}$ 的最小值；
    (2)为使流量最大，给出最佳设计方案．
    答案：(1) $2 \sqrt{2 S}$ ； $2 \sqrt[4]{3} \sqrt{S}$ (2)②

本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。