2023年高考数学新高考Ⅰ-9(5分)有一组样本数据$x_{1}$,$x_{2}$,$\dotsb$,$x_{6}$,其中$x_{1}$是最小值,$x_{6}$是最大值,则$($ $)$
A.$x_{2}$,$x_{3}$,$x_{4}$,$x_{5}$的平均数等于$x_{1}$,$x_{2}$,$\dotsb$,$x_{6}$的平均数
B.$x_{2}$,$x_{3}$,$x_{4}$,$x_{5}$的中位数等于$x_{1}$,$x_{2}$,$\dotsb$,$x_{6}$的中位数
C.$x_{2}$,$x_{3}$,$x_{4}$,$x_{5}$的标准差不小于$x_{1}$,$x_{2}$,$\dotsb$,$x_{6}$的标准差
D.$x_{2}$,$x_{3}$,$x_{4}$,$x_{5}$的极差不大于$x_{1}$,$x_{2}$,$\dotsb$,$x_{6}$的极差【答案详解】 |
2022年高考数学新高考Ⅱ-19(12分)在某地区进行流行病学调查,随机调查了100位某种疾病患者的年龄,得到如下的样本数据的频率分布直方图:
(1)估计该地区这种疾病患者的平均年龄(同一组中的数据用该组区间的中点值为代表);
(2)估计该地区一位这种疾病患者的年龄位于区间$[20$,$70)$的概率;
(3)已知该地区这种疾病的患者的患病率为$0.1%$,该地区年龄位于区间$[40$,$50)$的人口占该地区总人口的$16%$.从该地区中任选一人,若此人的年龄位于区间$[40$,$50)$,求此人患这种疾病的概率(以样本数据中患者的年龄位于各区间的频率作为患者的年龄位于该区间的概率,精确到0.0001 ).
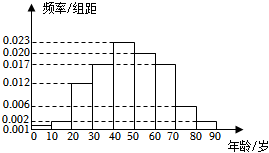 【答案详解】 【答案详解】 |
2022年高考数学新高考Ⅰ-20(12分)一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯(卫生习惯分为良好和不够良好两类)的关系,在已患该疾病的病例中随机调查了100例(称为病例组),同时在未患该疾病的人群中随机调查了100人(称为对照组),得到如下数据:
(1)能否有$99%$的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异?
(2)从该地的人群中任选一人,$A$表示事件“选到的人卫生习惯不够良好”, $B$表示事件“选到的人患有该疾病”, $\dfrac{P(B\vert A)}{P(\overline{B}\vert A)}$与$\dfrac{P(B\vert \overline{A})}{P(\overline{B}\vert \overline{A})}$的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为$R$.
(ⅰ)证明:$R=\dfrac{P(A\vert B)}{P(\overline{A}\vert B)}\cdot \dfrac{P(\overline{A}\vert \overline{B})}{P(A\vert \overline{B})}$;
(ⅱ)利用该调查数据,给出$P(A\vert B)$,$P(A\vert \overline{B})$的估计值,并利用(ⅰ)的结果给出$R$的估计值.
附:$K^{2}=\dfrac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| $P(K^{2}\geqslant k)$ | 0.050 | 0.010 | 0.001 | | $k$ | 3.841 | 6.635 | 10.828 |
【答案详解】 |
2021年高考数学新高考Ⅰ-18(12分)某学校组织“一带一路”知识竞赛,有$A$,$B$两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.$A$类问题中的每个问题回答正确得20分,否则得0分;$B$类问题中的每个问题回答正确得80分,否则得0分.
已知小明能正确回答$A$类问题的概率为0.8,能正确回答$B$类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.
(1)若小明先回答$A$类问题,记$X$为小明的累计得分,求$X$的分布列;
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.【答案详解】 |
2021年高考数学新高考Ⅰ-9(5分)有一组样本数据$x_{1}$,$x_{2}$,$\ldots$,$x_{n}$,由这组数据得到新样本数据$y_{1}$,$y_{2}$,$\ldots$,$y_{n}$,其中$y_{i}=x_{i}+c(i=1$,2,$\ldots$,$n)$,$c$为非零常数,则( )
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同
D.两组样本数据的样本极差【答案详解】 |

