．解答题
全国卷Ⅰ(理)
（20）（本小题满分12分）
设函数．
（Ⅰ）证明：
的导数
；
（Ⅱ）若对所有
都有
，求
的取值范围．
全国卷Ⅱ(理)
20．（本小题满分12分）
在直角坐标系
中，以
为圆心的圆与直线
相切．
（1）求圆
的方程；
（2）圆与
轴相交于
两点，圆内的动点
使
成等比数列，
求
的取值范围．
北京卷(理)
18．（本小题共13分）
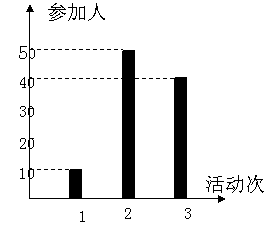某中学号召学生在今年春节期间至少参加一次社会公益活动（以下简称活动）．
该校合唱团共有100名学生，他们参加活动的次数统计如图所示．
（I）求合唱团学生参加活动的人均次数；
（II）从合唱团中任意选两名学生，求他们
参加活动次数恰好相等的概率．
（III）从合唱团中任选两名学生，
用
表示这两人参加活动次数之差的绝对值，
求随机变量
的分布列及数学期望
．
天津卷(理)
20．（本小题满分12分）
已知函数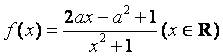
，其中
．
（Ⅰ）当
时，求曲线
在点
处的切线方程；
（Ⅱ）当
时，求函数
的单调区间与极值．
上海卷(理)
19．（本题满分14分）本题共有2个小题，第1小题满分7分，第2小题满分7分．
已知函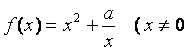数
，常数
．
（1）讨论函数
的奇偶性，并说明理由；
（2）若函数在
上为增函数，求
的取值范围．
辽宁卷(理)
20．（本小题满分14分）
已知正三角形
的三个顶点都在抛物线
上，其中为坐标原点，
设圆
是的内接圆（点为圆心）
（I）求圆的方程；
（II）设圆
的方程为
，过圆上任意一点分别作
圆的两条切线
，切点为
，求
的最大值和最小值．
江苏卷
20．（本题满分16分）
已知
是等差数列，
是公比为
的等比数列，
，
，
记
为数列
的前
项和．
（1）若
（
是大于
的正整数），求证：
；（4分）
（2）若
（
是某个正整数），求证：是整数，且数列
中的每一项
都是数列
中的项；（8分）
（3）是否存在这样的正数
，使等比数列
中有三项成等差数列？
若存在，写出一个的值，并加以说明；若不存在，请说明理由．（4分）
浙江卷(理)
（21）（本题15分）已知数列
中的相邻两项
是关于
的方程
的两个根，且
．
（I）求
，
，
，
；
（II）求数列
的前
项和
；
（Ⅲ）记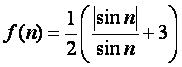
，
，
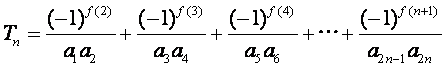求证：
．
福建卷(理)
20．（本小题满分12分）如图，已知点
，
直线
，
为平面上的动点，过
作直线
的垂线，垂足为点
，且
．
（Ⅰ）求动点
的轨迹
的方程；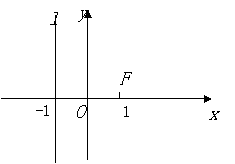
（Ⅱ）过点
的直线交轨迹
于
两点，交直线
于点
，
已知
，
，求
的值；
湖北卷(理)
19．（本小题满分12分）
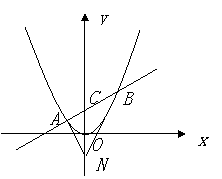
在平面直角坐标系
中，过定点
作直线与抛物线
（
）相交于
两点．
（I）若点
是点关于坐标原点的对称点，求
面积的最小值；
（II）是否存在垂直于
轴的直线，使得被以
为直径的圆截得的弦长恒为定值？
若存在，求出的方程；若不存在，说明理由．
（此题不要求在答题卡上画图）
湖南卷(理)
19．（本小题满分12分）
如图4，某地为了开发旅游资源，欲修建一条连接风景点和居民区的公路，
点所在的山坡面与山脚所在水平面
所成的二面角为
（
），且
，
点到平面的距离
（km）．沿山脚原有一段笔直的公路
可供利用．
从点到山脚修路的造价为
万元/km，原有公路改建费用为
万元/km．当山坡上
公路长度为
km（
）时，其造价为
万元．已知
，
，
，
．
（I）在
上求一点
，使沿折线
修建公路的总造价最小；
（II）
对于（I）中得到的点，在
上求一点
，使沿折线
修建公路的
总造价最小．
（III）在
上是否存在两个不同的点
，
，使沿折线
修建公路的总造
价小于（II）中得到的最小总造价，证明你的结论．
广东卷(理)
19．（本小题满分14分）
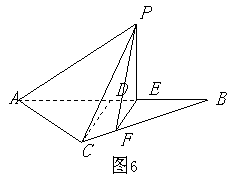如图6所示，等腰
的底边
，高
，点是线段
上异于点
的
动点，点
在
边上，且
，现沿
将
折起到
的位置，使
，
记
，
表示四棱锥
的体积．
（1）求
的表达式；
（2）当
为何值时，取得最大值？
（3）当取得最大值时，求异面直线与
所成角的余弦值．
重庆卷(理)
20．（本小题满分13分，其中（Ⅰ），（Ⅱ），（Ⅲ）小问分别为6，4，3分．）
已知函数
在
处取得极值
，其中
为常数．
（Ⅰ）试确定
的值；
（Ⅱ）讨论函数
的单调区间；
（Ⅲ）若对任意
，不等式
恒成立，求
的取值范围．
山东卷(理)
（20）（本小题满分12分）
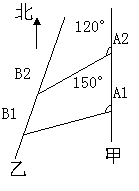如图，甲船以每小时
海里的速度向正北方航行，乙船按固定方向匀速直线
航行，当甲船位于
处时，乙船位于甲船的北偏西
方向的
处，此时两船
相距
海里，当甲船航行分钟到达
处时，
乙船航行到甲船的北偏西
方向
的
处，此时两船相距
海里，
问乙船每小时航行多少海里？
江西卷(理)
20．（本小题满分12分）
右图是一个直三棱柱（以
为底面）被一平面所截得到的几何体，截面为
．
已知
，
，
，
，
．
（1）设点是的中点，证明：
平面
；
（2）求二面角
的大小；
（3）求此几何体的体积．
陕西卷(理)
20．（本小题满分12分）
设函数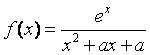
，其中
为实数．
（I）若
的定义域为
，求的取值范围；
（II）当
的定义域为时，求的单调减区间．
四川卷(理)
（20）（本小题满分12分）设
、
分别是椭圆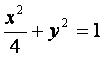
的左、右焦点.
（Ⅰ）若是该椭圆上的一个动点，求
·
的最大值和最小值;
（Ⅱ）设过定点
的直线与椭圆交于不同的两点
、
，且∠
为锐角
（其中
为坐标原点），求直线
的斜率
的取值范围.
安徽卷(理)
19．（本小题满分12分）
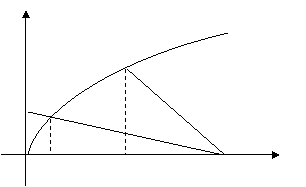如图，曲线
的方程为
．以原点为圆心．以
为半径的圆分别与
曲线
和
轴的正半轴相交于点
与点
．直线
与
轴相交于点
．
（Ⅰ）求点
的横坐标
与点的横坐标
的关系式
（Ⅱ）设曲线
上点
的横坐标为
，
求证：直线
的斜率为定值．
海南宁夏卷(理)
20．（本小题满分12分）
如图，面积为
的正方形
中有一个不规则的图形
，可按下面方法估计的
面积：在正方形
中随机投掷
个点，若个点中有
个点落入中，
则的面积的估计值为
，假设正方形的边长为2，
的面积为1，并向正方形中随机投掷
个点，
以
表示落入
中的点的数目．
（I）求的均值
；
（II）求用以上方法估计的面积时，
的面积的估计值与实际值之差
在区间
内的概率．
附表：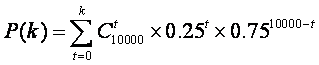
|
|
|
|
|
|
|
|
|
|
|
|
本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。
