三、解答题
19.(本小题满分12分)
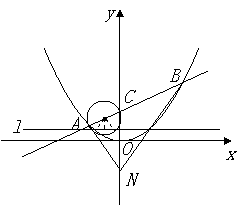
在平面直角坐标系![]() 中,过定点
中,过定点![]() 作直线与抛物线
作直线与抛物线![]() (
(![]() )
)
相交于![]() 两点.
两点.
(I)若点![]() 是点
是点![]() 关于坐标原点
关于坐标原点![]() 的对称点,求
的对称点,求![]() 面积的最小值;
面积的最小值;
(II)是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆截得的
为直径的圆截得的
弦长恒为定值?
若存在,求出![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
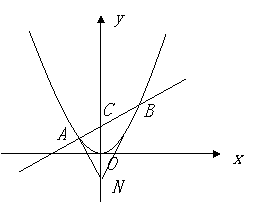
(此题不要求在答题卡上画图)
本小题主要考查直线、圆和抛物线等平面解析几何的基础知识,考查综合运用
数学知识进行推理运算的能力和解决问题的能力.
解法1:(Ⅰ)依题意,点![]() 的坐标为
的坐标为![]() ,可设
,可设![]() ,
,
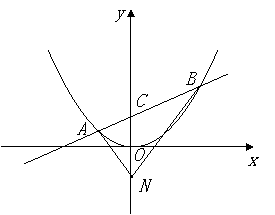 直线
直线![]() 的方程为
的方程为![]() ,与
,与![]() 联立得
联立得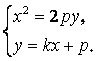 消去
消去![]() 得
得![]() .
.
由韦达定理得![]() ,
,![]() .
.
于是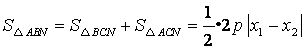 .
.
![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() .
.
(Ⅱ)假设满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ,
,
![]() 的中点为
的中点为![]() ,
,![]() 与
与![]() 为直径的圆相交于点
为直径的圆相交于点![]() ,
,![]() 的中点为
的中点为![]() ,
,
 则
则![]() ,
,![]() 点的坐标为
点的坐标为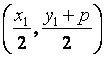 .
.
![]() ,
,
 ,
,
![]()
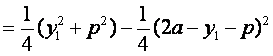
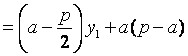 ,
,
![]()
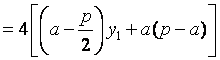 .
.
令![]() ,得
,得![]() ,此时
,此时![]() 为定值,故满足条件的直线
为定值,故满足条件的直线![]() 存在,
存在,
其方程为![]() ,
,
即抛物线的通径所在的直线.
解法2:(Ⅰ)前同解法1,再由弦长公式得
![]()
![]() ,
,
又由点到直线的距离公式得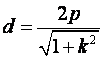 .
.
从而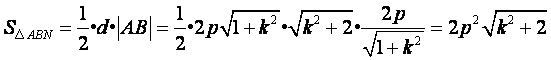 ,
,
![]() 当
当![]() 时,
时,![]() .
.
(Ⅱ)假设满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ,则以
,则以![]() 为直径的圆的方程为
为直径的圆的方程为![]() ,
,
将直线方程![]() 代入得
代入得![]() ,
,
则 .
.
设直线![]() 与以
与以![]() 为直径的圆的交点为
为直径的圆的交点为![]() ,
,
则有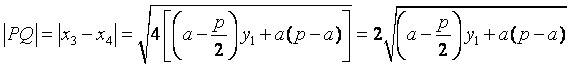 .
.
令![]() ,得
,得![]() ,此时
,此时![]() 为定值,故满足条件的直线
为定值,故满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ,
,
即抛物线的通径所在的直线.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。