三、命题趋势
    从上表可以看出，近几年本章考查呈现以下特点：

    1.题型和题量：一般有选择题(或填空题)，解答题中常把数学归纳法与数列等结合在一起考查，分值在10分左右．

    2.知识点考查：数列的极限和数学归纳法的考查较多，函数的极限与函数、闭区间上连续函数的性质结合在一起考查，成为对极限考查的新趋势．

    3.难度与创新：本章在高考中一般以选择、填空形式出现或渗透到解答题中，命题方向将逐步由求极限，直接用数列极限的四则运算法则求极限这些单一考查方面向结合等差(比)数列的计算求极限、结合无穷等比数列求和公式，结合数列求和方法求极限等一些综合考查方向过渡．

    四、复习建议
    根据本章知识的重要性以及高考对本章内容的考查情况，复习时应注意以下几个方面：

    1、深入理解极限的概念

    学习极限面临一个从“有限”到“无限”的飞跃．从数列或函数的变化趋势来理解极限问题是认识和解决问题的需要，也是学习中的难点，应给予足够重视．

    2、熟练运用四则运算法则求数列或函数的极限

    应用本章知识要解决的主要问题是在判断数列或函数极限存在的前提下，求极限值问题，特别是利用四则运算法则求数列或函数的极限．

    3、重视数学思想方法的复习

    数学归纳法是证明与自然数有关的命题的—种有效方法．要理解数学归纳法的原理及证题的方法步骤，特别是从假设`n=k`时命题成立，到`n=k+1`时，命题也成立的方法与技能．

    极限的思想方法：从有限中认识无限，从近似中认识精确，从量变中认识质变的这种极限思想贯穿在整章教材之中．

    抽象与概括、从特殊到一般是本章应用的一种主要思想方法，这方面在数列极限到函数极限的过渡以及各类形式极限的引入中均有体现．

    另外，还要特别注意“转化”这种数学思想方法的应用，它对帮助我们理解和解决有关问题非常有益 ．   

    五、思想与方法综览
    1、分类讨论的思想
　

    [案例]已知数列`{a_n}`、`{b_n}`都是由正数组成的等比数列，公比分别为`p`、`q`，其中`p>q`，且`p!=1`，`q!=1`，设`c_n``=``a_n`+`b_n`，`S_n=sum_(k=1)^nc_k`，求`lim_(n->oo)S_n/S_(n-1)`
    解:由已知得`S_n=(a_1(p^n-1))/(p-1)+(b_1(q^n-1))/(q-1)`

    `:.S_n/S_(n-1)=(a_1(q-1)(p^n-1)+b_1(p-1)(q^n-1))/(a_1(q-1)(p^(n-1)-1)+b_1(p-1)(q^(n-1)-1))`
    (1)当`0<p<1`时，`.:p>q`

    `:.0<q<1`

    `:.lim_(n->oo)S_n/S_(n-1)=(a_1(q-1)(0-1)+b_1(p-1)(0-1))/(a_1(q-1)(0-1)+b_1(p-1)(0-1))=1`

    (2)当`p>1`时，`.:p>q>0`

    `:.0<q/p<1`

    `:.lim_(n->oo)S_n/S_(n-1)=(a_1(q-1)(p-1/p^(n-1))+b_1(p-1)(q(q/p)^(n-1)-1/p^(n-1)))/(a_1(q-1)(1-1/p^(n-1))+b_1(p-1)((q/p)^(n-1)-1/p^(n-1)))`

    `=(a_1(q-1)(p-1)+b_1(p-1)(0-0))/(a_1(q-1)(1-0)+b_1(p-1)(0-0))=p`

    综上所述，`lim_(n->oo)S_n/S_(n-1)={(1，当0<p<1)，(0，当p>1):}`

    点评:本题的关键是如何正确寻找分类标准进行讨论，将问题转化为基本数列的极限去求解．
    当`p>1`时，不论`q>1`还是`0<q<1`，只要分子、分母同除以`p^(n-1)`，就可利用基本极限：`n->oo`，`q^n``->0`(`|q|<1`)．
　

    2、极限法
　

    [案例]已知`log_3x=(-1)/log_23`，那么`x+x^2+…+x^n+…=______`

    解:`.:log_3x=-log_32=log_3(1/2)`

    `:.x=1/2`

    `:.x+x^2+…+x^n+…=(1/2)/(1-1/2)=1`

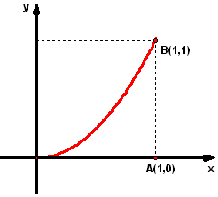
    答案：1
　

    [案例]如图，求抛物线`y=x^2`，`x`轴及直线所围成的图形面积．

    解:把底`AO``n`等分，每1小段长度为`1/n`，分点依次是`1/n`，`2/n`，…，`(n-1)/n`，在每小段上作1个矩形，使其左上角在抛物线上，矩形的高分别为对应点处的函数值`(i/n)^2(i=1，…，n-1)`，那么小矩形面积之和为：      

`S_n=(1/n)·(1/n)^2+(1/n)·(2/n)^2+…+(1/n)·((n-1)/n)^2``=1/n^3[1+2^2+3^2+…+(n-1)^2]`     `:.lim_(n->oo)S_n=lim_(n->oo)1/n^3[1+2^2+3^2+…+(n-1)^2]`     `=lim_(n->oo)((n-1)n(2n-1))/(6n^3)=1/3`     即要求图形的面积为`1/3`

    3、逆反思想
    很多问题正面求解往往困难重重，但若从反而思考，就会“柳暗花明”．
　

    [案例]已知`lim_(n->oo)3^n/(3^(n+1)+(a+1)^n)=1/3`，求`a`的取值范围．
    分析:分子、分母同除以`3^n`后，由`lim_(n->oo)((a+1)/3)^n=0`的充要条件求出`a`的范围．
    解:分式中的分子、分母同除以`3^n`，得`lim_(n->oo)3^n/(3^(n+1)+(a+1)^n)=lim_(n->oo)1/(3+((a+1)/3)^n)=1/3`
    `:.lim_(n->oo)((a+1)/3)^n=0`
    故此式成立的充要条件是`|(a+1)/3|<1`，解得`-4<a<2`

    一、知识结构
    (框图)

    二、知识梳理

    (一)知识要点
    1、数学归纳法证明命题的步骤．
    (1)证明当n取第一个值`n_0`(例如`n_0=1`或`2`等)时结论正确；
    (2)假设当`n=k(k∈N^**`，`k>=n_0`)时结论正确，证明当`n=k+1`时结论也正确．
    在完成了这两个步骤以后，就可以断定命题对于从`n_0`开始的所有正整数`n`都正确．
　

    2、数列极限与函数极限．
    (1)数列极限：如果当项数`n`无限增大时，无穷数列`{a_n}`的项`a_n`无限地趋近于一个常数`a`，那么就说数列`{a_n}`的极限是`a`，记作`lim_(n→∞)a_n=a`，或记作当`n→∞`时，`a_n→a`．
　

    (2)当`x→∞`时函数`f(x)`极限．
    ①当自变量`x`取正值并且无限增大时，如果函数`f(x)`无限趋近于一个常数`a`，就说当`x`趋向于正无穷大时，函数`f(x)`的极限是`a`，记作`lim_(x→+∞)f(x)=a`，或记作当`x→+∞`时，`f(x)→a`．
    ②当自变量`x`取负值并且绝对值无限增大时，如果函数`f(x)`无限趋近于一个常数`a`，就说当`x`趋向于负无穷大时，函数`f(x)`的极限是`a`，记作`lim_(x→-∞)f(x)=a`，或记作当`x→-∞`时，`f(x)→a`．
    ③如果`lim_(x→-∞)f(x)=lim_(x→+∞)f(x)=a`，则说当`x`趋向于无穷大时，函数`f(x)`的极限是`a`，记作`lim_(n→∞)f(x)=a`，或记作当`x→∞`时，`f(x)→a`．
　

    (3)当`x→x_0`时函数`f(x)`的极限．
    ①当自变量`x`无限趋近于常数`x_0`(但`x≠x_0`)时，如果函数`f(x)`无限趋近于一个常数`a`，就说当x趋近于`x_0`时，函数`f(x)`的极限是`a`，记作`lim_(x→x_0)f(x)=a`，或记作当`x→x_0`时，f(x)→a．
    ②如果当`x`从点`x=x_0`左侧(即`x<x_0`)无限趋近于`x_0`时，函数f(x)无限趋近于一个常数`a`，就说a是函数f(x)在点`x_0`处的左极限，记作`lim_(x→x_0^－)f(x)=a`．
    ③如果当`x`从点`x=x_0`右侧(即`x>x_0`)无限趋近于`x_0`时，函数`f(x)`无限趋近于一个常数`a`，就说`a`是函数`f(x)`在点`x_0`处的右极限，记作`lim_(x→x_0^＋)f(x)=a`.
    ④`lim_(x→x_0^－)f(x)=lim_(x→x_0^＋)f(x)=a hArr lim_(x→x_0)f(x)=a`．
　

    3、极限的四则运算法则．
    (1)如果`lim_(x→x_0)f(x)=a`，`lim_(x→x_0)g(x)=b`，那么
    `lim_(x→x_0)[f(x)+g(x)]=a+b`，`lim_(x→x_0)[f(x)g(x)]=a•b`，`lim_(x→x_0)f(x)/g(x)=a/b`．
    这些法则对于`x→∞`时的情况仍然成立．
    (2)如果`lim_(n→∞)a_n=a`，`lim_(n→∞)b_n=b`，那么
    `lim_(n→∞)[a_n±b_n]=a±b`，`lim_(n→∞)[a_n•b_n]=a•b`，`lim_(n→∞)a_n/b_n=a/b`．
　

    4、函数的连续性及其性质．
    (1)如果函数`y=f(x)`在点`x=x_0`处及其附近有定义，而且`lim_(x→x_0)f(x)=f(x_0)`，就说函数`f(x)`在点`x_0`处连续．
    (2)如果函数`f(x)`在开区间`(a，b)`内每一点处都连续，就说函数`f(x)`在开区间`(a，b)`内连续，或说`f(x)`是开区间`(a，b)`内的连续函数．
    (3)如果函数`f(x)`在开区间`(a，b)`内连续，在左端点`x=a`处有`lim_(x→x_0^＋)f(x)=f(a)`，在右端点`x=b`处有`lim_(x→x_0^－)f(x)=f(b)`，就说函数`f(x)`在闭区间`[a，b]`上连续．
    (4)连续函数性质(最大值最小值定理)
    如果`f(x)`是闭区间`[a，b]`上的连续函数，那么`f(x)`在闭区间`[a，b]`上有最大值和最小值．
　

    (二)考试要求
    1、了解数列极限和函数极限的概念．明确数列是特殊的函数，数列极限是特殊的函数极限，了解数列极限和函数极限之间的关系是特殊性与一般性问的关系．
    2、掌握数列极限和函数极限的四则运算法则，会灵活地应用于求某些比较简单的数列极限和函数极限．
    3、了解函数连续性的意义，理解函数极限与函数连续性概念间的联系，会用极限的方法判断函数的连续性．理解闭区间上的连续函数的最大值和最小值的性质定理，能应用于求闭区间上连续函数的最大值和最小值．
    4、理解数学归纳法的原理，能比较熟练地应用数学归纳法证明与自然数，`x`有关的比较简单的数学命题．
    5、本章渗透了从有限到无限，从近似到精确，从量变到质变的运动变化极限思想，特殊到一般的抽象、概括的思想，归纳、猜想、类比的思想，特别要会用“归纳、猜想、证明”的方法分析和解决有关的问题．
　

    (三)考点说明
    1、极限四则运算法则的变量可以由两个推广到有限个变量中去，不能推广到无穷多个．
    2、商的极限运算法则的前提是分子分母极限存在，且分母的极限不为零，否则要做分类考虑．
    如数列商的极限`lim_(n→∞)a_n/b_n`，
    若`lim_(n→∞)b_n=0，lim_(n→∞)a_n≠0`，则`lim_(n→∞)a_n/b_n=∞`；
    若`lim_(n→∞)b_n=0，lim_(n→∞)a_n=0`，则对`a_n/b_n`作适当的变形，使得分子或分母的极限至少有一个不为零后再求商的极限；
    若`lim_(n→∞)b_n=∞，lim_(n→∞)a_n=a`，则`lim_(n→∞)a_n/b_n=0`；
    若`lim_(n→∞)b_n=∞，lim_(n→∞)a_n=∞`，则对`a_n/b_n`作适当变形，使得分子或分母的极限至少有一个不为∞后再求商的极限．
    其中`lim_(n→∞)b_n=0，lim_(n→∞)a_n=0`，则其商的极限称为不定式`0/0`的极限；`lim_(n→∞)b_n=∞，lim_(n→∞)a_n=∞`，则其商的极限称为不定式`∞/∞`的极限．
    函数商的极限`lim_(n→∞)f(x)/g(x)、lim_(n→x_0)f(x)/g(x)`也有类似的情况，求极限时要特别注意．
    3、注意函数f(x)在点`x_0`处连续与函数f(x)在点`x_0`处有极限的区别与联系，函数f(x)在点`x_0`处有极限仅是函数f(x)在点`x_0`处连续的必要条件，不是充分必要条件．

    §13.2 函数的极限、连续性及其应用 (1)

    2、第一轮基础训练 (1) (2)

    3、第一轮单元训练 (1) (2)