|
一、复习目标 了解数列极限的概念,掌握极限的四则运算法则,会求某些数列的极限. 二、重点难点 三、特别提示 (1)应用数学归纳法要运用“归纳假设”,没有运用“归纳假设”的证明不是数学归纳法.
(2)证明代数恒等式的关键是:第二步将式子转化成与归纳假设的结构相同的形式——凑假设;然后利用归纳假设,经过恒等变形,得到结论所需要的形式——凑结论.
(3)证明三角恒等式时,常运用有关三角知识、三角公式,要掌握常用的三角变换方法.
(4)与正整数有关的不等式,有时也可用数学归纳法证明,在证明过程中,要运用不等式的性质.
(5)因为证明不等式的题型多种多样,所以不等式证明是一个难点,在由`n=k`时不等式成立推导`n=k+1`时不等式也成立时,过去讲过的证明不等式的方法在此都可以使用,如比较法、放缩法、分析法、反证法等,有时还要考虑与原不等式等价的命题.
(6)数列的极限是描述数列在无限变化过程中的变化趋势的重要概念,“随着项数`n`的无限增大,数列的项`a_n`无限地趋近某个常数`a`有两个方面的含义:一是过程性,即数列的项`a_n`趋近于`a`是在无限过程中进行的,也即随着`n`的增大,`a_n`越来越接近于`a`;二是无限性,即`a_n`不是一般地接近于`a`,而是“无限”地趋近于`a`,也即`|a_n-a|`随`n`的无限增大而无限地趋近于`0`.
(7)在运用数列极限的四则运算法则时要注意: ①参加运算的各数列的极限必须存在; ②作为除式的数列及其极限必须不为`0`; ③运算法则仅适用于求有限项的极限,而不适用于无限项的情况; ④当一个极限运算成立时,它的逆运算不一定成立,例如:`lim_(n->oo)(a_n+-b_n)`存在,并不一定有`lim_(n->oo)a_n`与`lim_(n->oo)b_n`都存在.
(8)求`lim_(n->oo)q^n`时,不可忽视对`q`的分类讨论. |
|
知识梳理 1、由一系列有限的特殊事例得出一般结论的推理方法叫归纳法.
2、数学归纳法 (2)假设当`n=k(kinN^*,k>=n_0)`时命题成立,并证明当`n=k+1`时,命题也成立,于是命题对一切`ninN^*`,`n>=n_0`,命题都成立 .这种证明方法叫做数学归纳法.
运用数学归纳法证明命题要分为两步,第一步是递推的
,第二步是递推的 ,这两步是缺一不可的.
3、数列极限的四则运算法则
4、常用的数列的极限 |
|
应用举例
二、案例示范 1、数列`{a_n}`前`n`项和记为`S_n`,已知`a_n=5S_n-3(ninN^*)`,求`lim_(n->oo)(a_1+a_3+…+a_(2n-1))`的值
2、`lim_(n->oo)((4/5-6/7)+(4/5^2-6/7^2)+…+(4/5^n-6/7^n))/((5/6-4/5)+(5/6^2-4/5^2)+…+(5/6^n-4/5^n))=______
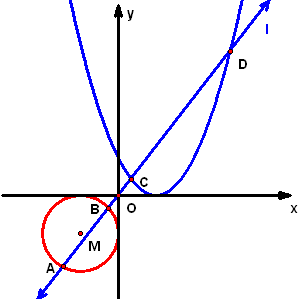
3、已知直线`l:x-ny=0(ninN)`,圆`M:(x+1)^2+(y+1)^2=1`,抛物线`varphi:y=(x-1)^2`,又`l`与`M`交于点`A`、`B`,`l`与`varphi`交于点`C`、`D`,求`lim_(n->oo)(|AB|^2/|CD|^2)`
|
|
实践体验 1、用数学归纳法证明`1/(1xx2)+1/(3xx4)+…+1/((2n-1)xx2n)=1/(n+1)+1/(n+2)+…+1/(n+n)`
2、求下列极限: (1)`lim_(n->oo)(2n^2+1)/(3n^2+2n)` (2)`lim_(n->oo)(sqrt(n^2+3n)-sqrt(n^2+4n))` (3)`lim_(n->oo)(1/n^2+4/n^2+7/n^2+…+(3n-2)/n^2)` (4)`lim_(n->oo)(2sin^nalpha+3cos^nalpha)/(sin^nalpha+cos^nalpha)`,`alphain[0,pi/2]`
|
|
拓展探究
|
|
|
|
|
学习感悟 2、常见的极限的类型和方法:(1)`0/0`型:分子分母通过分别求和化简等手段转化;(2)`(oo)/(oo)`型:分子分母同时除以`n`的最高次幂等化简转化;(3)已知极限值定参数:用待定系数法. 3、要注意极限运算法则的使用范围,特殊极限的使用条件,以及极限思想在实际问题中的应用. |