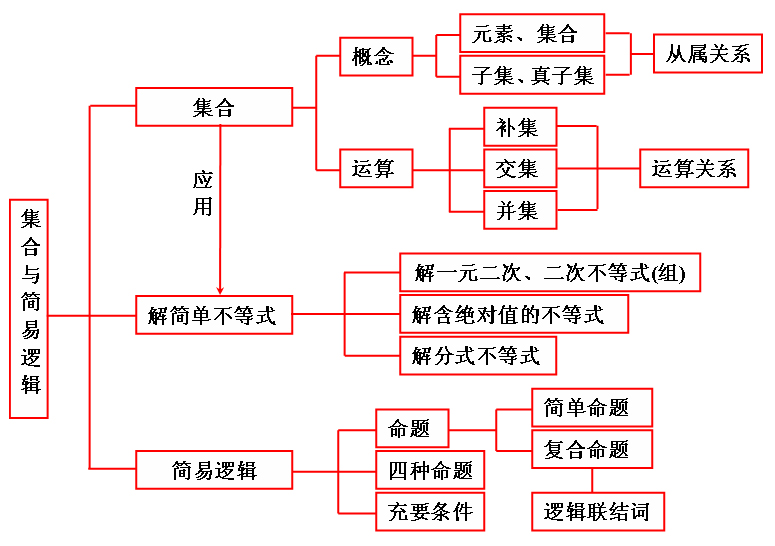
一、高考大纲
考试内容:
集合。子集。补集。交集。并集。
逻辑联结词。四种命题。充分条件和必要条件。
考试要求:
(1)理解集合、子集、补集、交集、并集的概念。了解空集和全集的意义。了解属于、包含、相等关系的意义。掌握有关的术语和符号,并会用它们正确表示一些简单的集合。
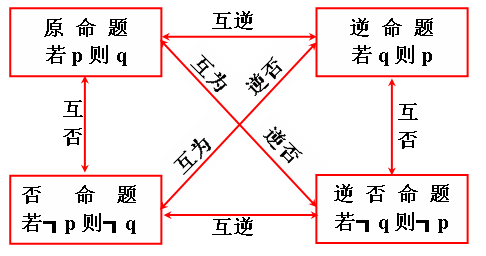
(2)理解逻辑联结词“或”、“且”、“非”的含义。理解四种命题及其相互关系。掌握充分条件、必要条件及充要条件的意义。
二、高考要览
| 考试内容 |
能力层次 |
高考要求 |
考题年份分值 |
| 集合与集合运算 |
理解 |
有关集合的概念和意义 |
|
2004 |
2005 |
2006 |
2007 |
2008 |
| 全国I.9 |
全国.5 |
全国Ⅱ1.5 |
|
|
| 全国Ⅱ.5 |
|
|
|
|
| 全国Ⅲ.10 |
|
|
|
|
| 全国Ⅳ.10 |
|
|
|
|
| 江苏.5 |
江苏.5 |
江苏7.5 |
|
|
| 北京.5 |
北京.5 |
|
|
|
| 天津.5 |
|
|
|
|
| 广东.5 |
广东.5 |
|
|
|
| 福建.5 |
|
福建4.5 |
|
|
| 湖北.9 |
湖北.5 |
|
|
|
| 浙江.5 |
|
浙江1.5 |
|
|
| 湖南.5 |
|
湖南1.5 |
|
|
| 安徽.5 |
|
|
|
|
| 上海春.5 |
上海.5 |
上海1.4 |
|
|
| |
江西.5 |
江西1.5 |
|
|
| |
北京春.12 |
|
|
|
| |
浙江.5 |
|
|
|
| |
|
四川1.5 |
|
|
| |
|
辽宁1.5 |
|
|
| |
|
安徽1.5 |
|
|
| |
|
重庆7.5 |
|
|
| |
|
山东1.5 |
|
|
|
| 掌握 |
有关术语和符号 |
| 逻辑联结词与四种命题 |
理解 |
逻辑联结词
"或""且""非"的含义;
四种命题及其相互关系. |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| |
|
广东5.5 |
|
|
| |
|
辽宁5.5 |
|
|
| |
|
山东16.4 |
|
|
| |
天津.5 |
|
|
|
| |
江苏.4 |
|
|
|
| 福建.5 |
|
|
|
|
|
| 充分条件与必要条件 |
掌握 |
充要条件的意义 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| |
|
上海14.5 |
|
|
| |
山东.5 |
山东8.5 |
|
|
| |
湖北.5 |
湖北8.5 |
|
|
| |
湖南.5 |
湖南4.5 |
|
|
| |
|
四川11.5 |
|
|
| |
|
天津4.5 |
|
|
| |
|
安徽4.5 |
|
|
| |
江西.5 |
|
|
|
| 重庆.5 |
重庆.5 |
|
|
|
| |
福建.5 |
|
|
|
| 浙江.5 |
|
|
|
|
| 辽宁.5 |
|
|
|
|
|
三、命题趋势
从上表可以看出,近几年高考在要间的考查呈现以下特点:
1、题型和题量:选择题为主,个别省市(主要是上海)涉及填空题,2004~2006三年(连同春招)共考查选择题34道、填空题5道,解答题仅2003年全国卷,2004年上海卷考过2道题,分值5~10分不等.
2、知识点考查:集中在集合的子、交、并补运算和命题中充要条件的考查,解不等式(含绝对值
及一元二次不等式)和集合概念逻辑联结词考查较少,而集合之间的运算以交、并特别是补集考查较多,命题考查以多选题为主,集中于充分、必要条件的判断.
3、难度与创新:集合与简易逻辑以中低档题为主,少量涉及创新的试题位置后移,使考生心理有缓冲,新定义型集合问题(如2006年四川T16,2006年广东T10,2006年辽宁T5)难度还是不算小的,充要条件与简易逻辑,估计会成为
今后创新的热点内容.
四、复习建议
《集合与简易逻辑》是整个高中阶段的起始内容,集合语言和充要条件贯穿高中学段的各章节之中,是基本数学语言和重要解题工具.
1、把握命题趋势
有关集合的试题,重点是集合与集合之间的关系,近几年试题加强了对集合的计算、化简,并向无限集发展.考查抽象思维能力,有关充要条件、命题真假的试题,侧重于概念的准确记忆和深层次的理解,试题以选择题居多,填空题往往是多项选择题,难度至多中等.
2、定位
集合的初步知识与简易逻辑知识,是掌握和使用数学语言的基础,集合语言广泛使用在数学中,应学会用集合观点去研究和解决数学问题;逻辑是研究思维形式及其规律的一门学科,是认识和研究问题的不可或缺的工具.
3、训练重点
理解集合中代表元素的真正意义,注意利用几何直观性帮助解题,画韦恩图,特殊值法解题,条件互推训练,充分、必要条件的判断,逻辑推理方面也应适当关注.
五、思想与方法综览
1、分类讨论思想
[案例]已知`A={x|x^2+(p+2)x+1=0,x∈R}`,`A nn
R^+=O/`,求实数p的取值范围(其中`R^+`表示正实数集).
解:`.: A nn R^+=O/,
`:. A`有三种情况:
①集合A中含有两个元素,且两个元素均为非正数,即方程`x^2+(p+2)x+1=0`有两个非正根,于是
`{(Delta=(p+2)^2-4>0 text(,)),(x_1+x_2=(p+2)<=0 text(,)rArr p>0),(x_1x_2=1>0):}`
②集合A中含有一个元素,即方程`x^2+(p+2)x+1=0`有两个相等的非正数解,于是`Delta=(p+2)^2-4=0`,
`:.` p=0或p=-4.
当p=0时,x=-1;当p=-4时,x=1,故p=0;
③集合A为空集,即方程`x^2+(p+2)x+1=0`无实根,于是`Delta=(p+2)^2-4<0`,得-4<p<0.
综合①②③,得p>-4.
2、等价转化思想
[案例]已知集合`A={(x,y)|y=-x^2+mx-1},B={(x,y)|x+y=3,0≤x≤3}`,若`A nn B`是单元素集,求实数m
的取值范围.
解:由`A nn B`是单元素集,得方程组
`{(y=-x^2+mx-1 text(,)),(x+y=3 text(.)):}`
(0≤x≤3)有且只有一组实数解.
消去y,问题即可转化为求方程`x^2-(m+1)x+4=0`在区间[0,3]上有且只有一个实数根时m的取值范围.
设`f(x)=x^2-(m+1)x+4=0`,则`f(0)=4,f(3)=10-3m`.
(1)由`f(0)f(3)<0,得m>10/3`.
(2)由`f(3)=0`,得`m=10/3`,这时方程另一解`x=4/3 in [0,3]`不合题意.
(3)抛物线与x轴相切时,△=0.
即`(m+1)^2-16=0`,
解得m=3,或m=-5(不合题意,舍去).
当m=3时,x=2∈[0,3].
综上所述,m的取值范围是`{3} uu (10/3,+oo).

点评:本例显然是有关集合的运算问题,但其实质是方程组在给定区间上解的个数问题(从解析几何的角度看,是抛物线与线段交点的个数问题),解题中,是将其转化为二次方程根的分布问题,使问题得以简捷的解决.因此,在解决数学问题时,要善于透过现象看本质,转化思维角度,变换问题形式,创造性地解决问题.
3、数形结合思想
[案例]求:(1)`f_3(x)=|x-1|+|x-2|+|x-3|`;
(2)`f_4(x)=|x-1|+|x-2|+|x-3|+|x-4|`的最小值.(注:`f_n(x)`指含有`n`个绝对值号的函数)

解:(1)`f_3(x)`的几何意义是x轴上的点x到点1,2,3的距离之和,
 显然由于|x-1|+|x-3|是点x到1,3的距离之和(不小于2,此时x∈[1,3]),只要|x-2|最小,即可`f_3(x)`取得最小值, 显然由于|x-1|+|x-3|是点x到1,3的距离之和(不小于2,此时x∈[1,3]),只要|x-2|最小,即可`f_3(x)`取得最小值,
因此当x=2时|x-1|+|x-2|+|x-3|的最小值是2.
(2)从(1)得到启示,求`f_4(x)`的最小值,应该考虑从距离最大的两端开始,
因为|x-1|+|x-4|的最小值为3(此时x∈[1,4]);|x-2|+|x-3|的最小值则为1(此时x∈[2,3]),
所以当x∈[2,3]时,`f_4(x)`有最小值3+1=4.
点评:考虑`f_5(x)=|x-1|+|x-2|+|x-3|+|x-4|+|x-5|`的最小值问题,则`f_5(x)`≥6,此时x=3;同理`f_n(x)=|x-1|+|x-2|+|x-3|+…+|x-n|`(n≥2,x∈N)的最小值,只要分n是偶数和奇数讨论可得`1+3+…+(n-1)=(n^2)/4`(n是偶数)或`2+4+…+(n-1)=(n^2-1)/4`(n是奇数).
所以`f_n(x)={((n^2-1)/4(n是奇数)),(n^2/4(n是偶数)):}`
另外,含绝对值的应用问题也是近年来高考的热点,如2004年北京卷T19、上海1998年东方航空杯数学竞赛题就是一道十分典例的实例.
4、函数与方程思想
[案例]已知集合`A={(x,y)|y=-3x+2,x∈N},B={(x,y)|y=a(x^2-x+1),x∈N)`,是否存在非零整数`a`,使`A nn B ≠O/`.
分析:通过构造方程或方程组求解.
解:由条件知集合A是由第四象限内的离散整数点及(0,2)构成的点集,集合B是抛物线`y=a(x^2-x+1)`上的
整数点集,因此问题转化为`{(y=-3x+2 text(,) ①),(y=a(x^2-x+1) ②):}`

是否存在非零整数`a`,使x有自然数解.
由①、②消去`y`得`ax^2+(3-a)x+a-2=0`.
`.:` x∈N,a≠0,从而有`Delta=(3-a)^2-4a(a-2)`≥0,
解得` (1-2sqrt(7))/3<=a<=(1+2sqrt(7))/3`
而`-2<(1-2sqrt(7))/3<-1,2<(1+2sqrt(7))/3<3`.又`a≠0`,
`:.``a`可能取值为-1,1,2,逐一代入检验知`a=-1`或`a=2`满足条件.
`:.`存在整数`a`等于-1或2,使`A nn B != O/`.
|