二、重点难点
    重点:逻辑联结词“或”、“且”、“非”的含义及其应用.

    难点:反证法及充要条件的意义与应用.

    三、特别提示
    1、“或”“且”“非”是判断简单命题与复合命题的依据，且它们分别与集合运算中的“并(集)”“交(集)”“补(集)”相对应．
    2、对一个命题进行否定，就是要对其中的关键词语进行否定，常见否定词句见下表：

正面词语 等于 大于(＞) 小于(＜) 是 都是 任意的 否定词语 不等于 不大于(≤) 不小于(≥) 不是 不都是 某个 正面词语 所有的 任意两个 至多有一个 至少有一个 至多有n个 否定词语 某些 某两个 至少有两个 一个也没有 至少有n+1个

    3、判断命题的真假要以真值表为依据，两个互为逆否的命题同真假，当一个命题的真假难以判断时，可考虑判断其等价命题的真假．
    4、在证明一个“若p则q”的命题为真时，要由条件户通过严密的逻辑推理得到结论q，而确定一个“若p则q”的命题为假时，一般可只举一个反例来说明命题为假．
    5、反证法体现了数学的转化思想，常用于以下问题的证明：①唯一性问题；②否定性问题；③“至多”或“至少”问题．

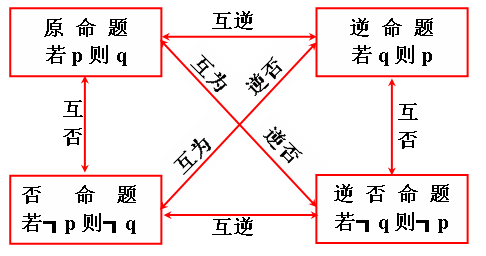
    3、 四种命题之间的相互关系.
   
    4、如果原命题为真，则原命题的逆否命题一定为真．
    5、欲证“若p则q”为真命题，从否定其结论即`not`q出发，经过正确的逻辑推理导出矛盾，从而`not`q为假，即原命题为真，这样的方法称为反证法．
    6、若p`rArr`q，那么p是q的充分条件，若q`rArr`p，那么p是q的必要条件．

    应用举例
    一、应用特点
    1、逻辑联结词“或”“且”“非”的含义；
    2、利用四种命题的关系判断一个命题的真假；
    3、运用反证法证明.

    二、案例示范
    (回味相关知识与方法，寻找解题办法，若有困难，可以参考“提示”，还有困难，可以参考“解答”或倾听老师的分析示范)

    1、已知命题p：方程`a^2x^2+ax-2=0`在[-1，1]上有解；命题q：只有一个实数x满足不等式`x^2+2ax+2a≤0`，若命题“p或q”是假命题，求a的取值范围.

提示	示范
先找出复合命题中的“或”“且”“非”，若没有，则根据前后意思填写出这些词即可.
解:由`a^2x^2+ax-2=O`，得(ax+2)(ax-1)=0，     显然`a≠0`，∴`x=-2/a或x=1/a`．     ∵x∈[-1，1]，故`|2/a|`≤1或`|1/a|`≤1，     ∴|a|≥1．     “只有一个实数满足`x^2+2ax+2a≤0`，即抛物线`y=x^2+2ax+2a`与x轴只有一个交点，     ∴△`=4a^2-8a=0`．∴a=O或2，     ∴命题“p或q为真命题”时“|a|≥1或a=0”     ∵命题“P或q”为假命题，     ∴a的取值范围为{a|-1＜a＜O或O＜a＜1}．     评注:理解“或”“且”“非”的含义是解题的关键，掌握复合命题真假的判断方法是非常必要的.

    2、写出下列命题的逆命题、否命题、逆否命题，并判断其真假．
    (1)全等三角形一定相似；
    (2)末位数字是零的自然数能被5整除．

提示	示范
解此题关键是分清原命题的条件和结论．命题(1)的题设是全等三角形，结论是相似三角形．命题(2)的题设是自然数的末住数字是零，结论是自然数能被5整除.
解:(1)逆命题：若两个三角形相似，则一定全等．逆命题为假．     否命题：若两个三角形不全等，则一定不相似．否命题为假．     逆否命题：若两个三角形不相似，则一定不全等．逆否命题为真．     (2)逆命题：若一个自然数能被5整除，则末位数字是零．逆命题为假．     否命题：若一个自然数的末位数字不是零，则不能被5整除．否命题为假．     逆否命题：若一个自然数不能被5整除，则末位数字不是零．逆否命题为真．     评注: 逆命题是将条件与结论对调，否命题是对条件的否定和对结论的否定，逆否命题即将条件和结论对调又对其进行否定．

    3、设二次函数`f(x)=ax^2+bx+c(a≠0)`中的a、b、c均为整数，且`f(0)、f(1)`均为奇数，求证：方程`f(x)=0`无整数根.

提示	示范
用反证法证明数学问题，首先要反设，即假设结论的反面成立．本题的反设为：假设方程有整数根．
解:假设方程`f(x)=0`有一个整数根k，则`ak^2+bk=-c`     又`f(0)=c，f(1)=a+b+c`均为奇数，所以`a+b`是偶数．     当`k`为偶数时，`-c=ak^2+bk`为偶数，与已知`f(0)=c`是奇数矛盾．     当`k`为奇数时，设`k=2n+1(n∈Z)`，则`-c=ak^2+bk=(2n+1)(2na+a+b)`为偶数，也与已知f(0)=c是奇数矛盾．     ∴方程`f(x)=0`无整数根.     评注:由题关于反证法证明命题“若p则q”的步骤:(1)否定欲证结论，假设它的反面成立；(2)进行正确推理，推出矛盾；(3)矛盾的出现说明结论的反面不成立，从而得出原结论成立．

    学习感悟
    1、逻辑联结词“或”“且”“非”的意义与日常生活中的“或”、“且”、“非”的意义不尽相同，三种复合命题与集合的并、交、补运算相呼应，因此可借助集合运算理解．
    2、判断命题的真假，判断充分与必要条件往往用反例(特殊值)来否定结论，还要注意使用集合的包含关系判定充分或必要条件．
    3、正难则反、涉及“至多”(至少)、“一定”(不一定)、“唯一”或否定等有关问题，往往用反证法．