二、重点难点
    重点:集合、子集、补集、交集、并集的概念及其表示.

    难点:含参数的集合问题的分析与解决.

    三、特别提示
    1、对于集合问题，要确定属于哪一类集合(数集、点集或某类图形)，然后再确定处理此类问题的方法．
    2、关于集合的运算，一般应把各参与运算的集合化到最简形式，再进行运算．
    3、含参数的集合问题，多根据集合的互异性处理，有时需要用到分类讨论、数形结合的思想．
    4、集合问题多与函数、方程、不等式有关，要注意各类知识的融会贯通．

    应用举例
    一、应用特点
    1、用集合的概念解题；
    2、用韦恩图解题；
    3、集合中交、并、补的运算.

    二、案例示范
    (回味相关知识与方法，寻找解题办法，若有困难，可以参考“提示”，还有困难，可以参考“解答”或倾听老师的分析示范)

    1、记函数`f(x)=sqrt(2-(x+3)/(x+1))`的定义域为`A`，`g(x)=text(lg)[(x-a-1)(2a-x)](a＜1)`的定义域为`B`.
    (1)求`A`；
    (2)若`B sube A`，求实数`a`的取值范围.

提示	示范
分别求出定义域为`A`、`B`是关键，但是`B`带有字母，注意讨论字母的取值范围.
解:(1)`2-(x+3)/(x+1)>=0，得(x-1)/(x+1)>=0，x＜-1`或`x>=1`，即`A=(-oo，-1)uu[1，+oo)`     (2)由`(x-a-1)(2a-x)＞0`，得     `(x-a-1)(x-2a)＜0`     `.: a＜1，:.a+1＞2a,:.B=(2a,a+1)`     `.:B sube A，:.2a>=1` 或 `a+1<=-1`，即 `a>=1/2` 或 `a<=-2`，而 `a＜1`     `:. 1/2<=a＜1`或 `a<=-2`，故当`B sube A`时，实数`a`的取值范围是`(-oo,-2)uu[1/2,1)`.     评注:对于`B sube A`，注意等价说法：`A uu B = A`或`A nn B = B`，集合中的元素具有确定性、互异性、无序性，特别是用互异性筛出不具备条件的元素是解题方法.

    2、如图所示，设`M`、`P`是两个非空集合，定义`M`与`P`的差集`M-P={x|x in M`且`x !in P}`则`M-(M-P)`等于(    ).
    A.`P`         B.`M nn P`        C.`M uu P`       D.`M`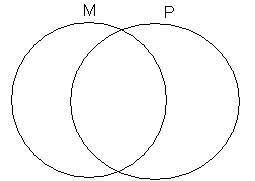
     

提示	示范
将题中的`M-P`用我们熟悉的交、并、补运算来表示，根据差集定义，“`x∈M`且`x!inP`”等价于“`x∈M nn C_UP`”.
解:设全集为U，则`M-P=M nn C_UP`．于是有`M-(M-P)=M-(M nn C_UP)=M nn C_U(M nn C_UP)`，由韦恩图可得`M-(M-P)=M nn P`．故选B．     答案:B     评注:这是一道新定义的集合运算迁移题．由于给出的新定义，以及所解决的问题中的集合都是抽象的集合．这时若类比于实数的运算，则得出错误结论．而用图示法，则有助于对新定义的理解．

    3、设全集`U={2，3，a^2+2a-3}`，`A={|2a-1|，2}，C_UA={5}`，求实数a的值.

提示	示范
`C_UA={5}`，它说明了两层含义，即`5∈U`，且`5!in A`，这样解题的思路和方法就很明显了.
解:`.:C_UA={5}`，`:.5∈U`，且`5!in A`     `:.a^2+2a-3=5`     解得`a=2`或`a=-4`     当`a=2`时，`|2a-1|=3≠5`；     当`a=-4`时，`|2a-1|=9≠5`，但`9!in U，:.a=2`．     评注:由题设条件求得`a=2`或`a=-4`后，验证其是否符合隐含条件`A sube U`是必要的，否则会把`n=-4`也误认为是本题的答案．集合是一种数学语言，如果不能从这种语言中破译出它的全部意义，就会出现失误．

    学习感悟
    1、对集合表示和认识，要以代表元素为切人点，首先明确元素的特性，再去看元素满足的条件．
    2、当集合元素用参数表示时，要注意集合元素的互异性．
    3、确定集合之间的关系，要充分利用集合元素的特征性质研究元素的构成．会借数轴，平面区域，图形等判断两个集合之间的包含关系，同时会利用`A sube B`，A=B等条件求集合中字母的值．利用`A sube B`求字母值时，不要忽略`A=O/`的情况，另外当B为有限集时可以列出A的所有情况求字母的值．利用A=B求字母值时，根据对应元素求出的值，要重新代入集合检验．
    4、辨析集合之间的关系应该从集合中元素的特点入手，将元素列举来直观发现，也可以从描述法中元素具备的
特性人手作定性分析，求同存异．
    5、空集和全集是特殊集合，应引起重视，必要时对集合是否为空集分类讨论，避免重复和遗漏．
    6、常用韦恩图直观表示集合之间的关系，或利用数轴和平面直角坐标系来反映集合及其关系．
    7、处理含参数的集合包含关系时，要注意端点值的取舍，必要时可单独考虑．