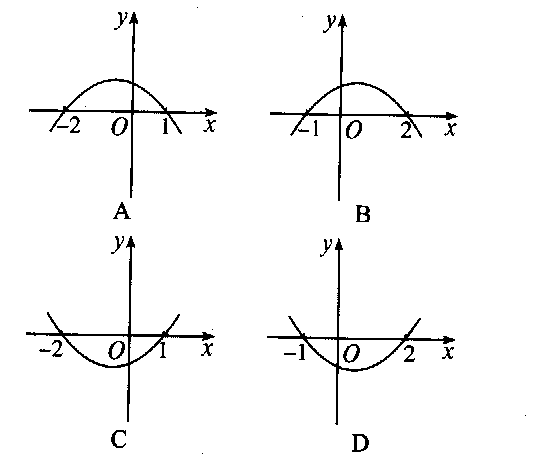|
一、复习目标 掌握简单的绝对值不等式的解法;掌握一元二次不等式的解法;学会运用函数方程、分类讨论、等价转化和数形结合思想解决有关不等式的问题. 二、重点难点 难点:含参绝对值不等式﹑一元二次不等式的解法. 三、特别提示 |
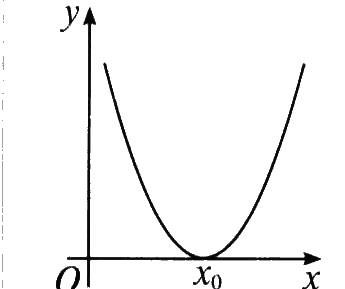
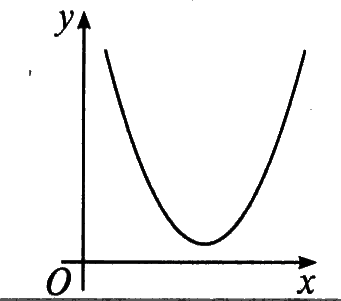
| 知识梳理 1、绝对值的意义:`|a|={(a (a>=0)),(-a (a<0)):}`. 2、绝对值不等式的解法 (1)当`a>0`时,`|x|>a hArr x^2>a^2 hArr x>a `或` x<-a;|x|<a hArr x^2<a^2 hArr -a<x<a` (2)当`a=0`时,不等式`|x|>a`的解集为`{x|x≠0}`,`|x|<a`的解集为`O/`. (3)当`a<0`时,不等式`|x|>a`的解集为`R`,`|x|<a`的解集为`O/`. (4)`c>0`时,`|ax+b|>c` `hArr` `ax+b>c` 或 `ax+b<-c` ,`|ax+b|<c` `hArr` `-c<ax+b<c` 3、一元二次不等式与二次函数、一元二次方程
4、已知a<b<c<d,不等式`((x-a)(x-c))/((x-b)(x-d))`≥O的解集是{x|x≤a,或b<x≤c,或x>d}. |
||||||||||||||||||||||||||||||
|
应用举例
二、案例示范 1、解不等式`3<|2x-3|<5`.
2、 解不等式`|x-1|+|x+2|<5`
3、已知不等式`ax^2+bx+c>0(a!=0)`的解集为`{x|alpha<x<beta,0<alpha<beta}`,求不等式`cx^2+bx+a<0`的解集.
|
| 实践体验 (在实践中提高能力,在体验中反思感悟,力求独立,力求提高) 1、解不等式: (1)`2<|2x-5|≤7`; (2)`x^2-2|x|-15≥0`.
2、已知函数`f(x)=(x^2)/(ax+b)(a`、`b`为常数),且方程`f(x)-x+12=0`有两个实根`x_1=3`,`x_2=4`. (1)求函数`f(x)`的解析式; (2)设`k>1`,解关于x的不等式:`f(x)<((k+1)x-k)/(2-x)`.
|
| 拓展探究 已知二次函数`f(x)`的二次项系数为`a`,且不等式`f(x)>-2x`的解集为`(1,3)`. (1)若方程`f(x)+6a=O`有两个相等的根,求`f(x)`的解析式; (2)若`f(x)`的最大值为正数,求a的取值范围.
|
|
|
|
|
学习感悟 |