|
平面向量的夹角公式<-->向量在物理中的应用举例
平面几何中的向量方法
向量在平面几何中的应用主要表现在平面几何问题的证明以及平面几何问题中的有关计算和几何图形形状的判断。
用向量法解决平面几何问题的“三步曲”是:
1 建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题。
2 通过向量运算,研究几何元素之间的关系。
3 把运算结果“翻译”成几何.
详解:向量集数形于一身,既有代数的抽象性又有几何的直观性,因此用向量的方法是几何研究的一个有力工具。而“三步曲”给出了利用向量的代数运算研究几何问题的基本思想。在解决平面几何问题时,将几何问题转化为向量问题是问题的关键。对于具体问题,是选用基向量法还是选用向量的坐标法是难点,利用向量的坐标法有时会给解决问题带来方便,在用向量解决证明时,一定要把向量结论转化为几何问题。
向量在解析几何中的应用,主要涉及直线中平行、垂直和求直线方程的问题,解题时一般是利用求轨迹的方法,先在直线上设一动点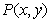 ,再根据条件建立关系。 ,再根据条件建立关系。
平面向量的夹角公式<-->向量在物理中的应用举例
全网搜索"平面几何中的向量方法"相关
|

