|
2023年高考数学天津17<-->2023年高考数学天津19
(15分)设椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a > b > 0)$的左、右顶点分别为$A_{1}$,$A_{2}$,右焦点为$F$,已知$\vert A_{1}F\vert =3$,$\vert A_{2}F\vert =1$.
(Ⅰ)求椭圆方程及其离心率;
(Ⅱ)已知点$P$是椭圆上一动点(不与顶点重合),直线$A_{2}P$交$y$轴于点$Q$,若△$A_{1}PQ$的面积是△$A_{2}FP$面积的二倍,求直线$A_{2}P$的方程.
答案:(Ⅰ)椭圆方程为$\dfrac{{x}^{2}}{4}+\dfrac{{y}^{2}}{3}=1$,椭圆的离心率为$e=\dfrac{c}{a}=\dfrac{1}{2}$;
(Ⅱ)直线$A_{2}P$的方程为$y=\pm \dfrac{\sqrt{6}}{2}(x-2)$.
分析:(Ⅰ)由题意可得$\left\{\begin{array}{l}{a+c=3}\\ {a-c=1}\end{array}\right.$,求解$a$与$c$的值,再由隐含条件求解$b$,则椭圆方程可求;
(Ⅱ)由题意可知,直线$A_{2}P$的斜率存在且不为0,设直线方程为$y=k(x-2)$,取$x=0$,得$Q(0,-2k)$,分别求出△$A_{1}PQ$的面积与△$A_{2}FP$面积,再由已知列式求解$k$,则直线方程可求.
解:(Ⅰ)由题意可知,$\left\{\begin{array}{l}{a+c=3}\\ {a-c=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\ {c=1}\end{array}\right.$,
$\therefore b^{2}=a^{2}-c^{2}=4-1=3$.
则椭圆方程为$\dfrac{{x}^{2}}{4}+\dfrac{{y}^{2}}{3}=1$,椭圆的离心率为$e=\dfrac{c}{a}=\dfrac{1}{2}$;
(Ⅱ)由题意可知,直线$A_{2}P$的斜率存在且不为0,
当$k < 0$时,直线方程为$y=k(x-2)$,取$x=0$,得$Q(0,-2k)$.
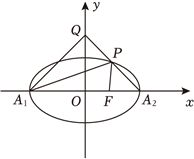
联立$\left\{\begin{array}{l}{y=k(x-2)}\\ {\dfrac{{x}^{2}}{4}+\dfrac{{y}^{2}}{3}=1}\end{array}\right.$,得$(4k^{2}+3)x^{2}-16k^{2}x+16k^{2}-12=0$.
△$=(-16k^{2})^{2}-4(4k^{2}+3)(16k^{2}-12)=144 > 0$,
$2{x}_{P}=\dfrac{16{k}^{2}-12}{4{k}^{2}+3}$,得${x}_{P}=\dfrac{8{k}^{2}-6}{4{k}^{2}+3}$,则${y}_{P}=\dfrac{-12k}{4{k}^{2}+3}$.
${S}_{\triangle {A}_{1}PQ}={S}_{\triangle {A}_{1}{A}_{2}Q}-{S}_{\triangle {A}_{1}{A}_{2}P}=\dfrac{1}{2}\times 4\times (-2k)-\dfrac{1}{2}\times 4\times (-\dfrac{12k}{4{k}^{2}+3})=\dfrac{-16{k}^{3}+12k}{4{k}^{2}+3}$.
${S}_{\triangle {A}_{2}FP}=\dfrac{1}{2}\times 1\times (-\dfrac{12k}{4{k}^{2}+3})=-\dfrac{6k}{4{k}^{2}+3}$.
$\therefore$$\dfrac{-16{k}^{3}+12k}{4{k}^{2}+3}=-\dfrac{12k}{4{k}^{2}+3}$,即$2k^{2}=3$,得$k=-\dfrac{\sqrt{6}}{2}(k < 0)$;
同理求得当$k > 0$时,$k=\dfrac{\sqrt{6}}{2}$.
$\therefore$直线$A_{2}P$的方程为$y=\pm \dfrac{\sqrt{6}}{2}(x-2)$.
点评:本题考查椭圆方程的求法,考查直线与椭圆位置关系的应用,考查运算求解能力,是中档题.
2023年高考数学天津17<-->2023年高考数学天津19
全网搜索"2023年高考数学天津18"相关
|

