|
2023年高考数学天津16<-->2023年高考数学天津18
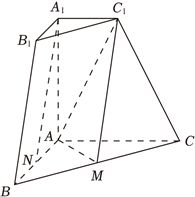
(15分)在三棱台$ABC-A_{1}B_{1}C_{1}$中,若$A_{1}A\bot$平面$ABC$,$AB\bot AC$,$AB=AC=AA_{1}=2$,$A_{1}C_{1}=1$,$M$,$N$分别为$BC$,$AB$中点.
(Ⅰ)求证:$A_{1}N//$平面$C_{1}MA$;
(Ⅱ)求平面$C_{1}MA$与平面$ACC_{1}A_{1}$所成角的余弦值;
(Ⅲ)求点$C$到平面$C_{1}MA$的距离.
答案:(Ⅰ)证明见解答;(Ⅱ)$\dfrac{2}{3}$;(Ⅲ)$\dfrac{4}{3}$.
分析:(Ⅰ)连接$MN$,推得四边形$MNA_{1}C_{1}$为平行四边形,再由平行四边形的性质和线面平行的判定定理可得证明;
(Ⅱ)运用三垂线定理得到平面$C_{1}MA$与平面$ACC_{1}A_{1}$所成角,再解直角三角形可得所求值;
(Ⅲ)运用等积法和三棱锥的体积公式可得所求距离.
解:

(Ⅰ)证明:连接$MN$,可得$MN$为△$AC$的中位线,
可得$MN//AC$,且$MN=\dfrac{1}{2}AC=1$,
而$A_{1}C_{1}=1$,$AC//A_{1}C_{1}$,
则$MN//A_{1}C_{1}$,$MN=A_{1}C_{1}$,
可得四边形$MNA_{1}C_{1}$为平行四边形,
则$A_{1}N//C_{1}M$,
而$A_{1}N\not\subset$平面$C_{1}MA$,$C_{1}M\subset$平面$C_{1}MA$,
所以$A_{1}N//$平面$C_{1}MA$;
(Ⅱ)取$AC$的中点$H$,连接$MH$,
由$AB\bot AC$,$MH//AB$,可得$MH\bot AC$.
由$A_{1}A\bot$平面$ABC$,$MH\subset$平面$ABC$,
可得$A_{1}A\bot MH$,
可得$MH\bot$平面$A_{1}ACC_{1}$.
过$H$作$HD\bot AC_{1}$,垂足为$D$,连接$DM$,
由三垂线定理可得$DM\bot AC_{1}$,
可得$\angle MDH$为平面$C_{1}MA$与平面$ACC_{1}A_{1}$所成角.
由$MH=\dfrac{1}{2}AB=1$.
在矩形$AHC_{1}A_{1}$中,$DH=\dfrac{AH\cdot H{C}_{1}}{A{C}_{1}}=\dfrac{1\times 2}{\sqrt{5}}=\dfrac{2\sqrt{5}}{5}$,
所以$\cos \angle MDH=\dfrac{DH}{DM}=\dfrac{\dfrac{2\sqrt{5}}{5}}{\sqrt{1+\dfrac{4}{5}}}=\dfrac{2}{3}$;
(Ⅲ)设$C$到平面$C_{1}MA$的距离为$d$.
在△$C_{1}MA$中,$A_{1}M=\dfrac{1}{2}AC=\sqrt{2}$,$AC_{1}=\sqrt{1+4}=\sqrt{5}$,$MC_{1}=\sqrt{1+4}=\sqrt{5}$,
则${S}_{\triangle {C}_{1}MA}=\dfrac{1}{2}\times \sqrt{2}\times \sqrt{5-\dfrac{1}{2}}=\dfrac{3}{2}$.
由${V}_{C-{C}_{1}MA}={V}_{{C}_{1}-CMA}$,可得$\dfrac{1}{3}d{S}_{\triangle {C}_{1}MA}=\dfrac{1}{3}d\cdot \dfrac{3}{2}=\dfrac{1}{3}C_{1}H\cdot S_{\Delta CMA}=\dfrac{1}{3}\times 2\times \dfrac{1}{2}\times 2\times 1=\dfrac{2}{3}$,
解得$d=\dfrac{4}{3}$.
点评:本题考查线面平行的判定和平面与平面所成角、点到平面的距离,考查转化思想和运算能力、推理能力,属于中档题.
2023年高考数学天津16<-->2023年高考数学天津18
全网搜索"2023年高考数学天津17"相关
|

