|
2023年高考数学上海春16<-->2023年高考数学上海春18
(14分)已知三棱锥$P-ABC$中,$PA\bot$平面$ABC$,$AB\bot AC$,$PA=AB=3$,$AC=4$,$M$为$BC$中点,过点$M$分别作平行于平面$PAB$的直线交$AC$、$PC$于点$E$,$F$.
(1)求直线$PM$与平面$ABC$所成角的大小;
(2)求直线$ME$到平面$PAB$的距离.
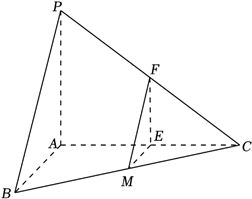
分析:(1)连接$AM$,$PM$,$\angle PMA$为直线$PM$与平面$ABC$所成的角,在$\Delta PAM$中,求解即可;
(2)先证明$AC\bot$平面$PAB$,可得$AE$为直线$ME$到平面$PAB$的距离.进则求$AE$的长即可.
解:(1)连接$AM$,$PM$,
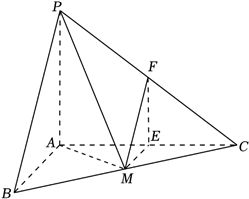
$\because PA\bot$平面$ABC$,
$\therefore \angle PMA$为直线$PM$与平面$ABC$所成的角,
在$\Delta PAM$中,$\because AB\bot AC$,$\therefore BC=\sqrt{{3}^{2}+{4}^{2}}=5$,
$\because M$为$BC$中点,$\therefore AM=\dfrac{1}{2}BC=\dfrac{5}{2}$,
$\therefore \tan \angle PMA=\dfrac{6}{5}$,即直线$PM$与平面$ABC$所成角为$\arctan \dfrac{6}{5}$;
(2)由$ME//$平面$PAB$,$MF//$平面$PAB$,$ME\bigcap MF=M$,
$\therefore$平面$MEF//$平面$PAB$,$\because ME\subset$平面$MEF$,$\therefore ME//$平面$PAB$,
$\because PA\bot$平面$ABC$,$AC\subset$平面$ABC$,
$\therefore PA\bot AC$,$\because AB\bot AC$,$PA\bigcap AB=A$,$PA$,$AB\subset$平面$PAB$,
$\therefore AC\bot$平面$PAB$,$\therefore AE$为直线$ME$到平面$PAB$的距离,
$\because ME//$平面$PAB$,$ME\subset$平面$ABC$,平面$ABC\bigcap$平面$PAB=AB$,
$\therefore ME//AB$,$\because M$为$BC$中点,$\therefore E$为$AC$中点,$\therefore AE=2$,
$\therefore$直线$ME$到平面$PAB$的距离为2.
点评:本题考查直线与平面所成的角,考查直线与平面的距离的求法,属中档题.
2023年高考数学上海春16<-->2023年高考数学上海春18
全网搜索"2023年高考数学上海春17"相关
|

